Nghiêm của phương trình sin2x = - sin x+ 2 là ...
Đọc tiếp
Nghiêm của phương trình sin2x = - sin x+ 2 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
3 tháng 2 2018
Đúng(0)
Những câu hỏi liên quan
PK
1
18 tháng 4 2016
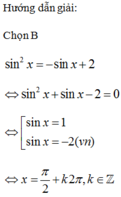
Điều kiện : \(\sin2x\ne0\Leftrightarrow x\ne\frac{k\pi}{2}\left(k\in Z\right)\)
\(\frac{3\sin x-2\sin x}{\sin2x\cos x2x}=2\Leftrightarrow3\sin x-2\sin x=2\sin2x.\cos x\)
\(\Leftrightarrow2\left(1-\cos x\right)\left(\sin2x-\sin x\right)=0\)
\(\Leftrightarrow\begin{cases}\cos x=1\\\sin2x=\sin x\end{cases}\)
\(\Leftrightarrow\begin{cases}x=2k\pi\\x=\frac{\pi}{3}+\frac{k2\pi}{3}\end{cases}\)
Đối chiếu với điều kiện ta có nghiệm của phương trình là \(x=\pm\frac{\pi}{3}+k2\pi\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
Xét phương trình \(sin\left( {x + \frac{\pi }{6}} \right) - sin2x = 0\;\)
\(\begin{array}{l} \Leftrightarrow sin\left( {x + \frac{\pi }{6}} \right) = sin2x.\\ \Leftrightarrow \left[ \begin{array}{l}x + \frac{\pi }{6} = 2x + k2\pi \\x + \frac{\pi }{6} = \pi - 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k2\pi \\x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
Với \(x = \frac{\pi }{6} + k2\pi \) có nghiệm dương bé nhất là \(x = \frac{\pi }{6}\) khi \(k = 0\).
Với \(x = \frac{{5\pi }}{{18}} + k\frac{{2\pi }}{3}\) có nghiệm dương bé nhất là \(x = \frac{{5\pi }}{{18}}\) khi \(k = 0\).
Vậy nghiệm dương bé nhất của phương trình đã cho là \(x = \frac{\pi }{6}\).
PT
1
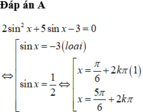
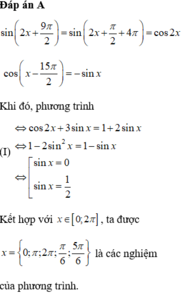
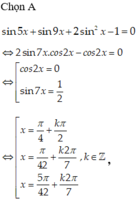
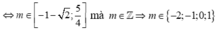
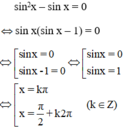
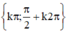(k ∈ Z).