Cho tam giác DEF cân tại D. Kẻ D H ⊥ E F ( H ∈ E F ) . a) Chứng minh H D E ^ = H D F ^...

PT

Pham Trong Bach

12 tháng 12 2017

Cho tam giác DEF cân tại D. Kẻ D H ⊥ E F ( H ∈ E F ) . a) Chứng minh H D E ^ = H D F ^ b) Kẻ H M ⊥ D E ( M ∈ D E ) và H N ⊥ ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

CM

Cao Minh Tâm

12 tháng 12 2017

Đúng(0)

NK

Ngọc Khuê

3 tháng 12 2021

Cho DEF vuông tại D. Đường cao DH. Chứng minh
a. \(\widehat{F}\)=H\(\widehat{D}\)E

b.\(\widehat{E}\)=H\(\widehat{D}\)F

#Hỏi cộng đồng OLM #Toán lớp 7

1

NH

Nguyễn Hoàng Minh

3 tháng 12 2021

\(a,\left\{{}\begin{matrix}\widehat{F}+\widehat{E}=90^0\\\widehat{HDE}+\widehat{E}=90^0\end{matrix}\right.\Rightarrow\widehat{F}=\widehat{HDE}\\ b,\left\{{}\begin{matrix}\widehat{F}+\widehat{E}=90^0\\\widehat{HDF}+\widehat{F}=90^0\end{matrix}\right.\Rightarrow\widehat{E}=\widehat{HDF}\)

Đúng(0)

PN

Phong Nguyễn

16 tháng 8 - olm

cho tam giác ABC nhọn nối tiếp đường tròn o, các đường cao AD,BE,CF cắt nhau tại H. chứng minh

a) các điểm A,E,H,F;B,D,H,F;C,D,H,E;B,C,E,F;A,B,D,E;A,C,D,F cùng thộc một đường tròn (6 ý riêng)

#Hỏi cộng đồng OLM #Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

16 tháng 8

Xét tứ giác AEHF có \(\hat{AEH}+\hat{AFH}=90^0+90^0=180^0\)

nên AEHF là tứ giác nội tiếp

=>A,E,H,F cùng thuộc một đường tròn

Xét tứ giác BDHF có \(\hat{BDH}+\hat{BFH}=90^0+90^0=180^0\)

nên BDHF là tứ giác nội tiếp

=>B,D,H,F cùng thuộc một đường tròn

Xét tứ giác HDCE có \(\hat{HDC}+\hat{HEC}=90^0+90^0=180^0\)

nên HDCE là tứ giác nội tiếp

=>H,D,C,E cùng thuộc một đường tròn

Xét tứ giác BFEC có \(\hat{BFC}=\hat{BEC}=90^0\)

nên BFEC là tứ giác nội tiếp

=>B,F,E,C cùng thuộc một đường tròn

Xét tứ giác AFDC có \(\hat{AFC}=\hat{ADC}=90^0\)

nên AFDC là tứ giác nội tiếp

=>A,F,D,C cùng thuộc một đường tròn

Xét tứ giác BDEA có \(\hat{BDA}=\hat{BEA}=90^0\)

nên BDEA là tứ giác nội tiếp

=>B,D,E,A cùng thuộc một đường tròn

Đúng(0)

NT

Nguyễn Thái Sơn

8 tháng 5 2020 - olm

Cho tam giác ABC. Kẻ AH vuông góc BC ( H thuộc BC). Gọi D, E, F lần lượt là
các điểm nằm giữa A và H, nằm giữa B và H, nằm giữa C và H. Chứng minh rằng
chu vi tam giác DEF nhỏ hơn chu vi tam giác ABC. Với vị trí nào của các điểm D,
E, F thì chu vi tam giác DEF bằng ½ chu vi tam giác ABC.

Giúp với mik sắp phải nộp bài rồi

#Hỏi cộng đồng OLM #Toán lớp 7

0

LT

Lê Tường Vân

14 tháng 5 2022 - olm

Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC tại H(H€BC)
a) chứng minh tam giác ABH= tam giác ACH
b) trên tia đối của CA lấy E sao cho CA=CE, AH cắt BE tại D. Chứng minh tam giác DBC cân
c) CD cắt AB tại F. chứng minh DF=2C Mình cần gấp ạ, cảm on

#Hỏi cộng đồng OLM #Toán lớp 7

0

HM

HOÀNG MINH KHÔI

3 tháng 3 2020 - olm

Cho tam giác DEF cân tại D. Gọi H là trung điểm của EF. a) C/m: t/giác DEH = t/giác DFH và DH vuông góc EF b) Kẻ HM vuông góc DE tại M, HN vuông góc DF tại N. C/m: t/giác HMN cân tại H c) C/m: MN// EF d) Qua E kẻ đường thẳng d vuông góc với DE, qua F kẻ đường thẳng d' vuông góc với DF, đường thẳng d cắt đường thẳng d' tại K. C/m: D, H , K thẳng hàng.

#Hỏi cộng đồng OLM #Toán lớp 7

1

HB

Hạt Bụi Thiên Thần

14 tháng 4 2020

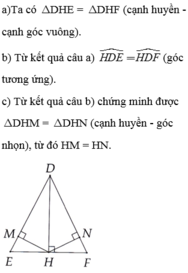
a) Xét tam giác DEH và tam giác DFH ta có:

DE = DF ( tam giác DEF cân tại D )

DEH = DFH ( tam giác DEF cân tại D )

EH = EF ( H là trung điểm của EF )

=> tam giác DEH = tam giác DFH ( c.g.c) (dpcm)

=> DHE=DHF(hai góc tương ứng)

Mà DHE+DHF=180 độ =>DHE=DHF=180 độ / 2 = 90 độ ( góc vuông ) hay DH vuông góc với EF ( dpcm )

b) Xét tam giác MEH và tam giac NFH ta có:

EH=FH(theo a)

MEH=NFH(theo a)

=> tam giác MEH = tam giác NFH ( ch-gn)

=> HM=HN ( 2 cạnh tương ứng ) hay tam giác HMN cân tại H ( dpcm )

c) Ta có : +) DM+ME=DE =>DM=DE-ME

+) DN+NF=DF => DN=DF-NF

Mà DE=DF(theo a) ; ME=NF( theo b tam giác MEH=tam giác NFH)

=>DM=DN => tam giác DMN cân tại D

Xét tam giac cân DMN ta có:

DMN=DNM=180-MDN/2 (*)

Xét tam giác cân DEF ta có:

DEF=DFE =180-MDN/2 (*)

Từ (*) và (*) Suy ra góc DMN = góc DEF

Mà DMN và DEF ở vị trí đồng vị

=> MN//EF (dpcm)

d) Xét tam giác DEK và tam giác DFK ta có:

DK là cạnh chung

DE=DF(theo a)

=> tam giác DEK= tam giác DFK(ch-cgv)

=>DKE=DKF(2 góc tương ứng)

=>DK là tia phân giác của góc EDF (1)

Theo a tam giac DEH= tam giac DFH(c.g.c)

=>EDH=FDH(2 góc tương ứng)

=>DH là tia phân giác của góc EDF (2)

Từ (1) và (2) Suy ra D,H,K thẳng hàng (dpcm)

Đúng(0)

T

thanimtje

7 tháng 3 2022

Bài 10. Cho tam giác DEF vuông tại D, có . Tia phân giác của góc F cắt DE tại I. Kẻ IH vuông góc với EF tại H ( ). a. Chứng minh: DFI = HFI b. DFH là tam giác gì? Vì sao?. c. Qua E kẻ đường thẳng vuông góc với DH tại N. Chứng minh EN // FI. Bài 11. Cho cân ở A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE. a) Chứng minh cân b) Gọi M là trung điểm của BC. Chứng minh AM là tia...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

1

NL

Nguyễn Lê Phước Thịnh

7 tháng 3 2022

Bạn ghi lại đề đi bạn

Đúng(0)

T

thanimtje

7 tháng 3 2022

Bài 10. Cho tam giác DEF vuông tại D, có . Tia phân giác của góc F cắt DE tại I. Kẻ IH vuông góc với EF tại H ( ).

a. Chứng minh: DFI = HFI

b. DFH là tam giác gì? Vì sao?.

c. Qua E kẻ đường thẳng vuông góc với DH tại N. Chứng minh EN // FI.

Bài 11. Cho cân ở A. Trên tia đối của các tia BC và CB lấy thứ tự hai điểm D và E sao cho BD = CE.

a) Chứng minh cân

b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của .

c) Từ B và C kẻ BH, CK theo thứ tự vuông góc với AD và AE Chứng minh: BH = CK.

d) Chứng minh ba đường thẳng AM, BH, CK đồng quy. Đây ạ

Đúng(0)

ND

Nguyễn Đức An

17 tháng 5 2020 - olm

Cho tam giác DEF cân D (\(\widehat{D}\)< \(^{90^o}\) ). Kẻ DH vuông góc EF tại Ha) Chứng minh tam giác DHE=tam giác DHF \(\widehat{EDH}\)=\(\widehat{FDH}\)b) Kẻ EM vuông góc DF (\(M\)E\(DF\)), FN vuông góc DE(\(N\)E\(DE\)). Chứng minh tam giác DMN là tam giác cânc) EM cắt FN tại O. Chứng minh ba điểm D,O,H thẳng hàng.d)Qua F kẻ đường thẳng song song với EM, cắt tia DH tại P; tam giác DEF phải thỏa mãn điều kiện gì để tam giác...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 7

0

NT

Nguyen Tien Hoc

26 tháng 2 2022

cho tam giác abc cân tại a gọi h là trung điểm của bc

a, Chứng minh AH vuông góc với BC

b, Kẻ HE vuong góc với AB tại E ; HF vuông góc với AC tại F . Chứng minh HE = HF

c, Chứng minh tam giác AEF là tam giác cân

d, Chứng minh EF song song BC

#Hỏi cộng đồng OLM #Toán lớp 7

1

DT

Đỗ Tuệ Lâm

26 tháng 2 2022

undefined

Đúng(2)

NT

Nguyen Tien Hoc

26 tháng 2 2022

bạn ơi mờ quá

Đúng(1)

KT

KIỆT TRẦN MINH

9 tháng 10 2021

cho tam giác ABC vuông tại A có đường cao Ah Gọi E là điểm đối xúng của H qua AB và F là điểm đối xúng cuẩ H qua AC . Chứng Minh :
a/tam giác AHE cân
b/ Ba điểm E , A ,F thẳng hàng
c/ BC= BE+CF
d/tam giác EMF cân với M là trung điểm của BC

#Hỏi cộng đồng OLM #Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 10 2021

a: Ta có: H và E đối xứng nhau qua BA

nên AB là đường trực của HE

Suy ra: AH=AE

hay ΔHAE cân tại H

Đúng(1)

KT

KIỆT TRẦN MINH

8 tháng 10 2021

cho tam giác ABC vuông tại A có đường cao Ah Gọi E là điểm đối xúng của H qua AB và F là điểm đối xúng cuẩ H qua AC . Chứng Minh :
a/tam giác AHE cân
b/ Ba điểm E , A ,F thẳng hàng
c/ BC= BE+CF
d/tam giác EMF cân với M là trung điểm của BC

#Hỏi cộng đồng OLM #Toán lớp 8

1

RH

Rin Huỳnh

8 tháng 10 2021

1A; 2B; 3B; 4D; 5A

Đúng(0)

KT

KIỆT TRẦN MINH

8 tháng 10 2021

????

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP