Biết rằng đồ thị hàm số cắt trục hoành Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số cắt trục hoành Ox tại bao nhiêu điểm?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()

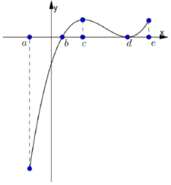
Ta có bảng biến thiên như hình vẽ sau:
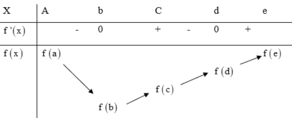
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.

Ta có
![]()
Đồ thị hàm số ![]() cắt trục hoành tại bốn điểm phân biệt bên phương trình
cắt trục hoành tại bốn điểm phân biệt bên phương trình ![]() , với
, với ![]() là các nghiệm.
là các nghiệm.
Suy ra
![]()
![]()
![]()
![]()
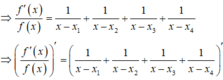
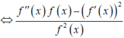
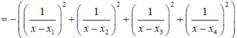
Nếu ![]() với
với ![]() thì
thì ![]() ,
, ![]()
![]() .
.
Nếu ![]() thì
thì 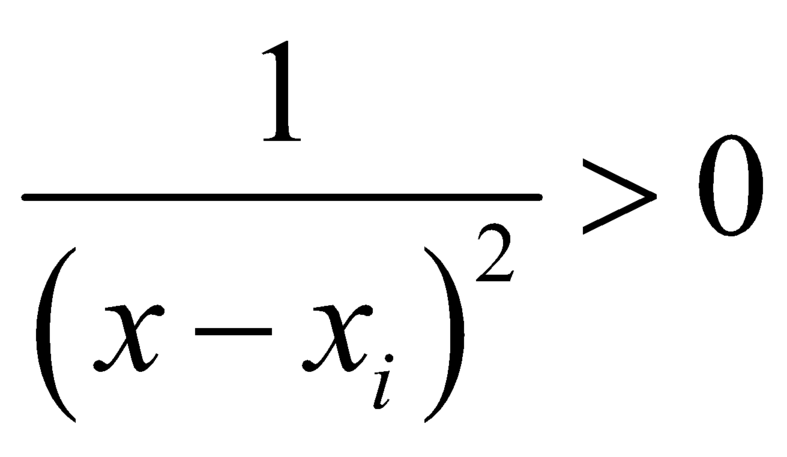 ,
, ![]() .
.
Suy ra ![]()
![]() .
.
Vậy phương trình ![]() vô nghiệm hay phương trình
vô nghiệm hay phương trình ![]() vô nghiệm.
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A


Cái câu vẽ đồ thị thì bạn chỉ cần lập bảng giá trị rồi biễu diễn trên hệ trục tọa độ Oxy là được

a: Các điểm B;D thuộc đồ thị, còn A,C không thuộc đồ thị
b: Thay y=-1 vào y=1/3x, ta được:
1/3x=-1
hay x=-3
Vậy: E(-3;-1)
Thay x=-4 vào y=1/3x, ta được:
y=-1/3x4=-4/3
Vây: F(-4;-4/3)

a: Thay x=10 và y=-15 vào f(x), ta được:
10m-20=-15
=>10m=5
hay m=1/2


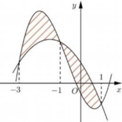
Đáp án B
Giả thiết
Đặt
thì
Và
Khi đó, phương trình
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.