Trong không gian Oxyz, cho tam giác nhọn ABC có H(2;2;1), , O lần lượt là hình chiếu vuông góc của A, B, C trên các cạnh BC, AC, AB. Đường thẳng d qua A và vuông góc với mặt phẳng (ABC) có phương trình là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.

Đáp án A
- Cách 1: Giả sử H(x;y;z) là trực tâm của tam giác ABC, ta có điều kiện sau:
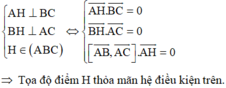
Do nhận xét được AB → . AC → = 0 ⇒ AB → ⊥ AC → nên ta tìm được cách giải độc đáo sau:
- Cách 2: Vì tam giác ABC vuông tại A nên trực tâm H của tam giác ABC trùng với điểm A
- Lời giải chi tiết cho cách 2: AB → = − 1 ; 0 ; 1 ; AC → = 1 ; 1 ; 1 , nhìn nhanh thấy
AB → . AC → = 0 ⇒ AB ⊥ AC nên tam giác ABC vuông tại A và A là trực tâm


Ta có : \(\overrightarrow{AB}=\left(-a;b;0\right)\)
và \(\overrightarrow{AC}=\left(-a;0;c\right)\)
Vì \(\overrightarrow{AB}.\overrightarrow{AC}=a^2>0\) nên góc \(\widehat{BAC}\) là góc nhọn
Lập luận tương tự chứng minh được các góc \(\widehat{B}\) và \(\widehat{C}\) cũng là góc nhọn

Đáp án A
Gọi D là chân đường phân giác góc B của tam giác ABC . Theo tính chất đường phân giác ta có : 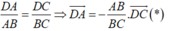
![]()
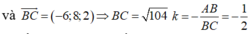
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ
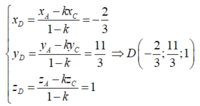
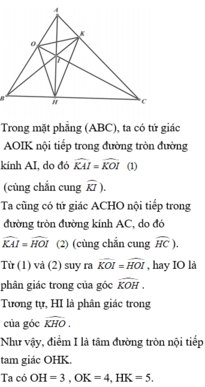

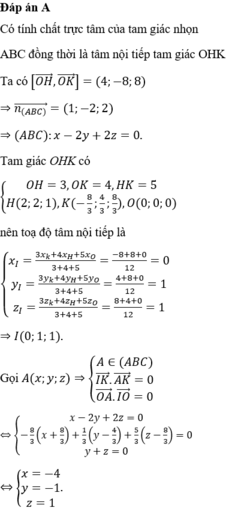



Ta có tứ giác BOKC là tứ giác nội tiếp đường tròn suy ra O K B ^ = O C B ^ 1
Ta có tứ giác KDHC là tứ giác nội tiếp đường tròn suy ra D K H ^ = O C B ^ 2
Do đó BK là đường phân giác trong của góc O K H ^ và AC là đường phân giác ngoài của góc O K H ^ .
Tương tự ta chứng minh được OC là đường phân giác trong của góc K O H ^ và AB là đường phân giác ngoài của góc K O H ^
Chọn D