Cho và là hai phương trình của hai dao động điều hòa cùng phương. Biết phương trình của dao động tổng hợp là . Để tổng biên độ của các dao động thành phần cực đại thì có giá trị là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bài ra ta có
Z C = 50 Ω ; I = 120/50 = 2,4 (A)
i = 2,4 2 cos(100 π t + π /2) (A)

Theo bài ra ta có
Z C = 5 Ω ; I = 120/5 = 24 (A)
i = 24 2 cos(1000 π t + π /2) (A)

Xem giản đồ Fre-nen (H.III.5G)
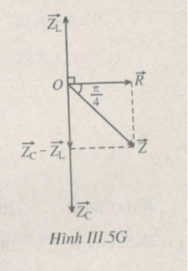
Z L = ω L = 100 π .1/10 π = 100 Ω
Z C = 1/ ω C = 20 Ω
![]()
U = U L 2 = 20 2
⇒ u = 40cos(100 π t - π /4)

Theo bài ra ta có
Z L = 50 Ω ; I = 120/50 = 2,4 (A)
i = 2,4 2 cos(100 π t - π /2) (A)
Đáp án B
Phương pháp: Sử dụng giản đồ vecto và định lí hàm số sin trong tam giác
Cách giải:
- Phương trình dao động của x ; x 1 ; x 2 : x = 5 cos ω t + φ x 1 = A 1 cos ω t + π 3 x 2 = A 2 cos ω t − π 4
Suy ra:
+ Độ lệch pha giữa x và x 1 là π 3 − φ
+ Độ lệch pha giữa x và x 2 là φ + π 4
+ Độ lệch pha giữa x 1 và x 2 là π 3 − − π 4 = 7 π 12
Ta có giản đồ vecto:
- Áp dụng định lí hàm số sin trong tam giác ta có:
A sin 5 π 12 = A 1 sin ( φ + π 4 ) = A 2 sin ( π 3 − φ ) → A 1 = A sin φ + π 4 sin 5 π 12 A 2 = A sin π 3 − φ sin 5 π 12
→ A 1 + A 2 = A sin φ + π 4 sin 5 π 12 + A sin π 3 − φ sin 5 π 12 = A sin 5 π 12 sin φ + π 4 + sin π 3 − φ
- Có: s i n a + s i n b = 2 sin a + b 2 . c os a − b 2 ⇒ sin φ + π 4 + sin π 3 − φ = 2 sin 7 π 24 c os φ − π 24
⇒ A 1 + A 2 = 2 A sin 7 π 24 sin 5 π 12 . c os φ − π 24
Để [ A 1 + A 2 ] đạt cực đại thì: c o s φ − π 24 max = 1 ⇒ φ − π 24 = k 2 π ⇒ φ = π 24