Cho dãy số (un) có số hạng đầu và thỏa mãn . Biết với mọi n ≥ 1 Giá trị nhỏ nhất của n để bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Dễ thấy un là cấp số nhân với q = 10
Ta có: u8 = 107u1; u10 = 109u1
Do đó PT ![]()
![]()
![]()
Giải PT ta được logu1 = -17 ⇔ u1 = 10-17 ⇒ u2018 = 102017 u1 = 102000

Đáp án B.
Đặt t = 2 + log u 1 - 2 log u 10 ≥ 0
⇔ 2 log u 1 - 2 log u 10 = t 2 - 2 ,
khi đó giả thiết trở thành:
log u 1 - 2 log u 10 + 2 + log u 1 - 2 log u 10 = 0
⇔ t 2 + t - 2 = 0
<=> t = 1 hoặc t = -2
⇒ log u 1 - 2 log u 10 = - 1
⇔ log u 1 + 1 = 2 log u 10
⇔ log 10 u 1 = log u 10 2 ⇔ 10 u 1 = u 10 2 ( 1 )
Mà un+1 = 2un => un là cấp số nhân với công bội q = 2
=> u10 = 29 u1 (2)
Từ (1), (2) suy ra
10 u 1 = 9 9 u 1 2 ⇔ 2 18 u 1 2 = 10 u 1 ⇔ u 1 = 10 2 18
⇒ u n = 2 n - 1 . 10 2 18 = 2 n . 10 2 19 .
Do đó u n > 5 100 ⇔ 2 n . 10 2 19 > 5 100
⇔ n > log 2 5 100 . 2 19 10 = - log 2 10 + 100 log 2 5 + 19 ≈ 247 , 87
Vậy giá trị n nhỏ nhất thỏa mãn là n = 248.

Đáp án C
Phương pháp : Áp dụng công thức :
tanα.cotα = 1ó tanα(tan900 – α) = 1
Cách giải : Ta có : ![]() >P = tan10.tan20.tan30…tan890
>P = tan10.tan20.tan30…tan890
óP=(tan10.tan890).(tan20.tan880).(tan30.tan870)…tan450
óP=(tan10.cot10).(tan20.cot20).(tan30.cot30)…..(tan440.cot440).tan450
óP=1.1.1…..1=1 =>logP = log1 = 0

\(u_n=2u_{n-1}+3n-1\)
\(\Leftrightarrow u_n+3n+5=2\left(u_{n-1}+3\left(n-1\right)+5\right)\)
Đặt \(u_n+3n+5=v_n\Rightarrow\left\{{}\begin{matrix}v_1=10\\v_n=2v_{n-1}\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội 2
\(\Rightarrow v_n=10.2^{n-1}\Rightarrow u_n+3n+5=10.2^{n-1}\)
\(\Leftrightarrow u_n=10.2^{n-1}-3n-5\)
\(\Rightarrow u_{2019}=10.2^{2018}+3.2019-1=...\)

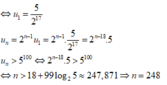
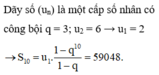
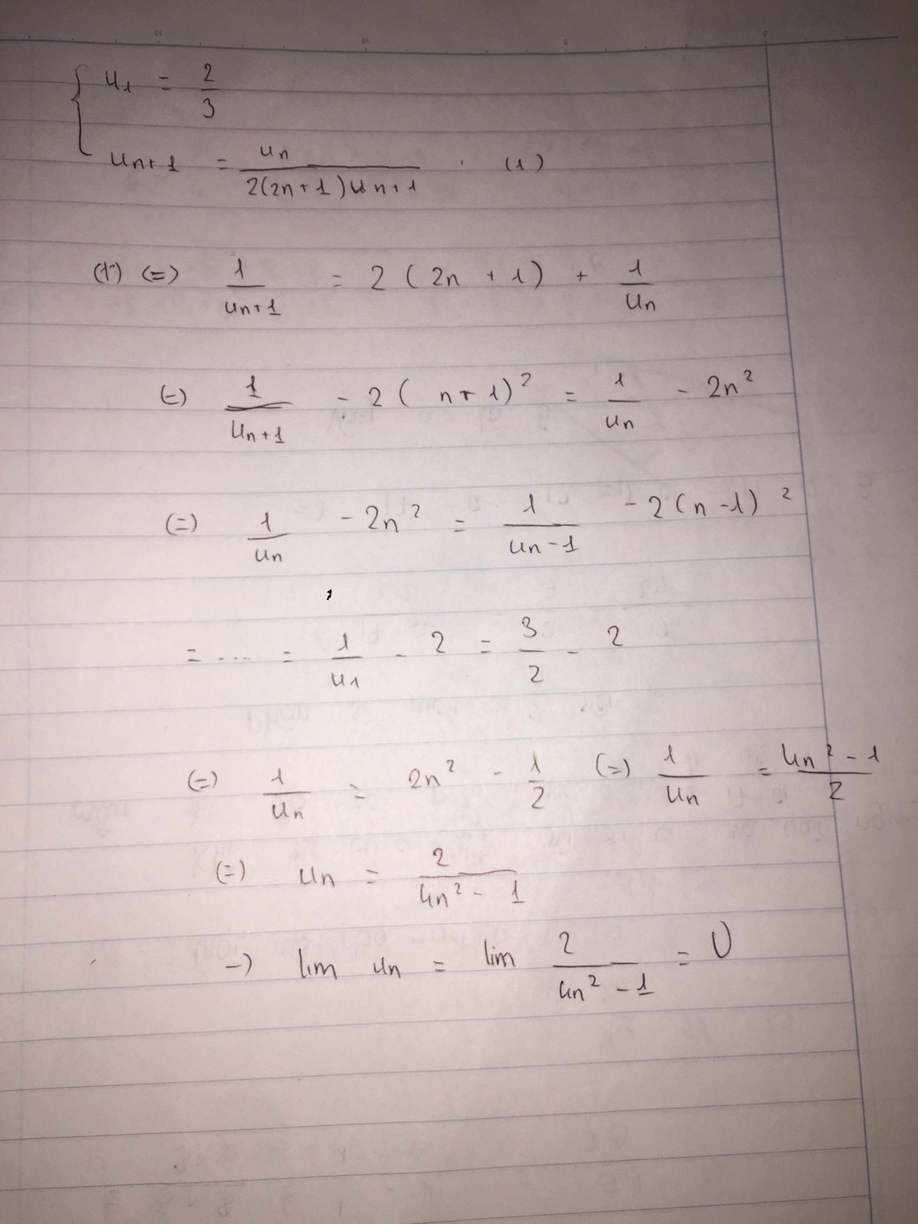
Chọn đáp án D