Cho tích phân , giả sử đặt . Tìm mệnh đề đúng.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left\{{}\begin{matrix}u=x^2\\dv=cos2xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2xdx\\v=\dfrac{1}{2}sin2x\end{matrix}\right.\)
\(\Rightarrow I=\dfrac{1}{2}x^2sin2x|^{\pi}_0-\int\limits^{\pi}_0x.sin2xdx\)

d) \(\sqrt[]{x}>x\)
\(\Leftrightarrow x-\sqrt[]{x}< 0\)
\(\Leftrightarrow\sqrt[]{x}\left(\sqrt[]{x}-1\right)< 0\left(x\ge0\right)\)
\(\Leftrightarrow0< x< 1\)
a) \(P\left(x\right):"x^2-5x+4=0"\)
\(x^2-5x+4=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{1;4\right\}\) để \(P\left(x\right):"x^2-5x+4=0"\) đúng
b) \(P\left(x\right):"x^2-5x+6=0"\)
\(x^2-5x+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{2;3\right\}\) để \(P\left(x\right):"x^2-5x+6=0"\) đúng
c) \(P\left(x\right):"x^2-3x=0"\)
\(x^2-3x=0\)
\(\Leftrightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
Vậy \(x\in\left\{0;3\right\}\) để \(P\left(x\right):"x^2-3x=0"\) đúng
d) \(P\left(x\right):"\sqrt[]{x}>x"\)
\(\sqrt[]{x}>x\)
\(\Leftrightarrow x-\sqrt[]{x}< 0\)
\(\Leftrightarrow\sqrt[]{x}\left(\sqrt[]{x}-1\right)< 0\)
\(\Leftrightarrow0< x< 1\)
Vậy \(x\in\left(0;1\right)\) để \(P\left(x\right):"\sqrt[]{x}>x"\) đúng
e) \(P\left(x\right):"2x+3< 7"\)
\(2x+3< 7\)
\(\Leftrightarrow2x< 4\)
\(\Leftrightarrow x< 2\)
Vậy \(x\in(-\infty;2)\) để \(P\left(x\right):"2x+3< 7"\) đúng
f) \(P\left(x\right):"x^2+x+1>0"\)
\(x^2+x+1>0\)
\(\Leftrightarrow x^2+x+\dfrac{1}{4}+\dfrac{3}{4}>0\)
\(\Leftrightarrow\left(x+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
\(\Leftrightarrow\forall x\in R\) để \(P\left(x\right):"x^2+x+1>0"\) đúng

Chọn C.
Phương pháp : Đưa biểu thức đã cho về dạng y ' y = g x và lấy nguyên hàm hai vế.
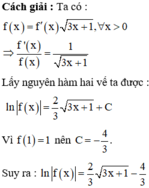
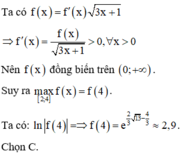
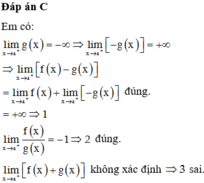
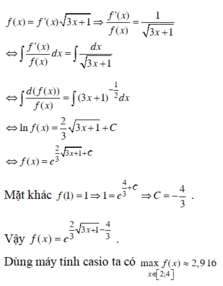
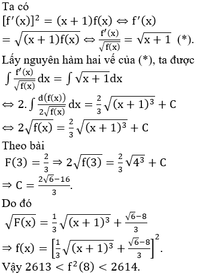
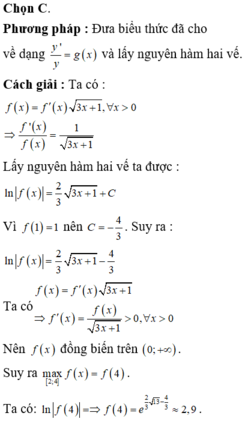
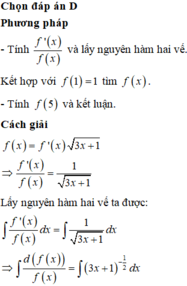
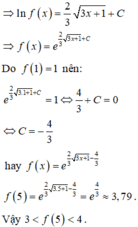
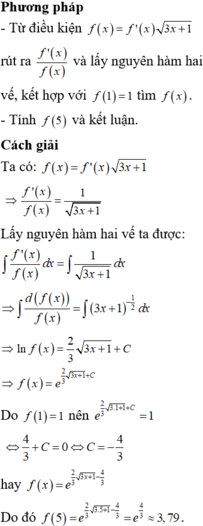
Đáp án A