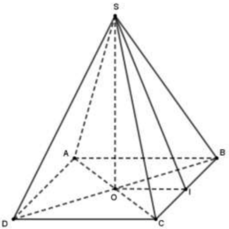
Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành tâm O; mặt phẳng vuông góc với mặt phẳng . Biết khoảng cách từ O đến mặt phẳng lần lượt là 1;2; . Tính khảng cách d từ O đến mặt phẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
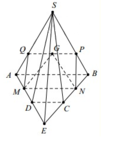
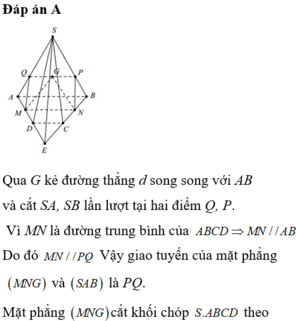
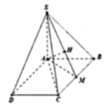
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .

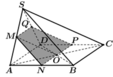
Tham khảo hình vẽ bên.
Gọi P, Q lần lượt là trung điểm của CD, SD. Khi đó thiết diện tạo bởi mặt phẳng (OMN) với hình chóp là hình thang MNPQ. Thật vậy:
![]()
Chọn B.

+) Xét tam giác SAC có SA = SC \( \Rightarrow \) SAC là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) AC.
Xét tam giác SBD có SB = SD \( \Rightarrow \) SBD là tam giác cân mà SO là trung tuyến
\( \Rightarrow \) SO \( \bot \) BD.
+) Ta có SO \( \bot \) AC; SO \( \bot \) BD; AC \( \cap \) BD tại O \( \Rightarrow \) SO \( \bot \) (ABCD).

Đáp án: D.
Hướng dẫn giải:
Lấy M là trung điểm BC, H là hình chiếu của A lên SM. Xác định
![]()
S A ⊥ B C ⊥ A M
![]()
⇒ A H ⊥ S M ⇒ A H ⊥ ( S B C )
⇒ d ( A , ( S B C ) ) = A H
Vì AD//(SBC) chứa BC nên
d(SB,AD)=d(AD,(ABC))=d(A,(SBC))=AH
Tính: SA=AD= a 2 ,AM= a 2
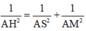
⇒ A H = a 2 5

Chọn C.
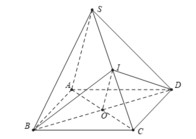
+) Ta có:
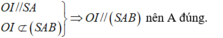
+) Ta có:
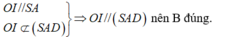
+) Ta có: mp (IBD) cắt hình chóp theo thiết diện là tam giác IBD nên C sai.
+) Ta có: (IBD) ∩ (SAC) = IO nên D đúng.

Đáp án C
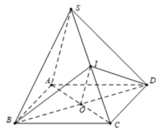
Ta có: O I / / S A O I ∉ S A B ⇒ O I / / S A B nên A đúng
Ta có: O I / / S A O I ∉ S A D ⇒ O I / / S A D nên B đúng
Ta có: (IBD)cắt hình chóp theo thiết diện là tam giác IBD nên
Ta có: I B D ∩ S A C = I O nên D đúng.


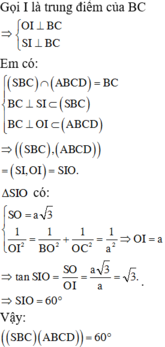

Chọn đáp án A
Cách 1:
Lấy mặt phẳng α vuông góc với SO cắt (SAC), (SBD) theo các giao tuyến x’Ox, y’Oy.
Chọn hệ tọa độ Oxyz sao cho tia Oz trùng với tia OS
Cách 2:
Trong mặt phẳng (SAC) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SA, SC lần lượt tại A’, C’
Trong mặt phẳng (SBD) dựng đường thẳng qua O vuông góc với đường thẳng SO cắt hai đường thẳng SB, SD lần lượt tại B’, D’
Khi đó tứ diện OSA’B’ có OS, OA’, OB’ đôi một vuông góc nên ta chứng minh được