Cho khối hộp . Gọi M là trung điểm của AB. Mặt phẳng chia khối hộp đã cho thành hai phần. Gọi là thể tích khối đa diện có chứa và là thể tích phần còn lại. Tính tỉ số .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

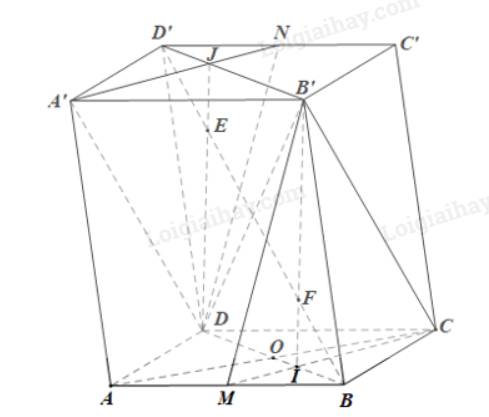
a)
Ta có: (ADD’A’) // (CBC’B’);
(ADD’A’) ∩ (DCB’A’) = A’D;
(CBC’B’) ∩ (DCB’A’) = B’C.
Do đó A’D // B’C, mà B’C ⊂ (B’CM) nên A’D // (B’CM).
Tương tự: (ABB’A’) // (DCC’D’);
(ABB’A’) ∩ (DMB’N) = MB’;
(DCC’D’) ∩ (DMB’N) = DN.
Do đó MB’ // DN, mà MB’ ⊂ (B’CM) nên DN // (B’CM).
Ta có: A’D // (B’CM);
DN // (B’CM);
A’D, DN cắt nhau tại điểm D và cùng nằm trong mp(A’DN)
Do đó (A’DN) // (B’CM).
b)
Trong mp(A’B’C’D’), gọi J là giao điểm của A’N và B’D’.
Trong mp(BDD’B’), D’B cắt DJ tại E.
Ta có: D’B ∩ DJ = {E} mà DJ ⊂ (A’DN) nên E là giao điểm của D’B và (A’DN).
Tương tự, trong mp(ABCD), gọi I là giao điểm của CM và BD.
Trong mp(BDD’B’), D’B cắt B’I tại F.
Ta có: D’B ∩ B’I = {F} mà B’I ⊂ (B’CM) nên F là giao điểm của D’B và (B’CM).
• Ta có: (A’DN) // (B’CM);
(A’DN) ∩ (BDD’B’) = DJ;
(B’CM) ∩ (BDD’B’) = B’I.
Do đó DJ // B’I.
Trong mp(BDD’B’), xét DBDE có IF // DE nên theo định lí Thalès ta có: \(\frac{{BI}}{{BD}} = \frac{{BF}}{{BE}}\) (1)
Trong mp(ABCD), gọi O là giao điểm của hai đường chéo AC và BD trong hình bình hành ABCD. Khi đó O là trung điểm của AC, BD.
Xét ∆ABC, hai đường trung tuyến BO, CM cắt nhau tại I nên I là trọng tâm của tam giác
Suy ra \(\frac{{BI}}{{BO}} = \frac{2}{3}\) hay \(\frac{{BI}}{{\frac{1}{2}BD}} = \frac{{2BI}}{{BD}} = \frac{2}{3}\)
Do đó \(\frac{{BI}}{{BD}} = \frac{1}{3}\) (2)
Từ (1) và (2) suy ra \(\frac{{BF}}{{BE}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\).
Chứng minh tương tự ta cũng có \(\frac{{D'E}}{{D'F}} = \frac{{D'J}}{{D'B'}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\)
Do đó \(\frac{{BF}}{{EF}} = \frac{{D'E}}{{EF}} = \frac{1}{2}\) nên BF = D’E = ½ EF.

Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).

a)
Xét tam giác ABI vuông tại A và tam giác CDI vuông tại C có:
AI = CI (I là trung điểm của AC)
AB = CD (gt)
=> Tam giác ABI = Tam giác CDI (cạnh huyền - cạnh góc vuông)
b)
=> AIB = CID (2 góc tương ứng)
mà AIB + BIC = 1800 (2 góc kề bù)
=> BIC + CID = 1800
=> BIC và CID là 2 góc kề bù
=> BI và ID là 2 tia đối
=> B, I, D thẳng hàng
mà BI = ID (Tam giác ABI = Tam giác CDI)
=> I là trung điểm của BD
c)
Xét tam giác BIC và tam giác DIA có:
BI = ID (Tam giác ABI = Tam giác CDI)
BIC = DIA (2 góc đối đỉnh)
IC = IA (I là trung điểm của AC)
=> Tam giác BIC = Tam giác DIA (c.g.c)
=> BC = AD (2 cạnh tương ứng)
d)
CP = BC : 2 (P là trung điểm của BC)
AQ = AD : 2 (Q là trung điểm của AD)
mà BC = AD (theo câu c)
=> CP = AQ
Xét tam giác AQI và tam giác CPI có:
IA = IC (I là trung điểm của AC)
IAQ = ICP (Tam giác BIC = Tam giác DIA)
AQ = CP (chứng minh trên)
=> Tam giác AQI = Tam giác CPI (c.g.c)
=> AIQ = CIP (2 góc tương ứng)
mà CIP + PIA = 1800 (2 góc kề bù)
=> PIA + AIQ = 1800
=> PIA và AIQ là 2 góc kề bù
=> PI và IQ là 2 tia đối
=> P, I, Q thẳng hàng
mà PI = IQ (Tam giác AQI = Tam giác CPI)
=> I là trung điểm của PQ.
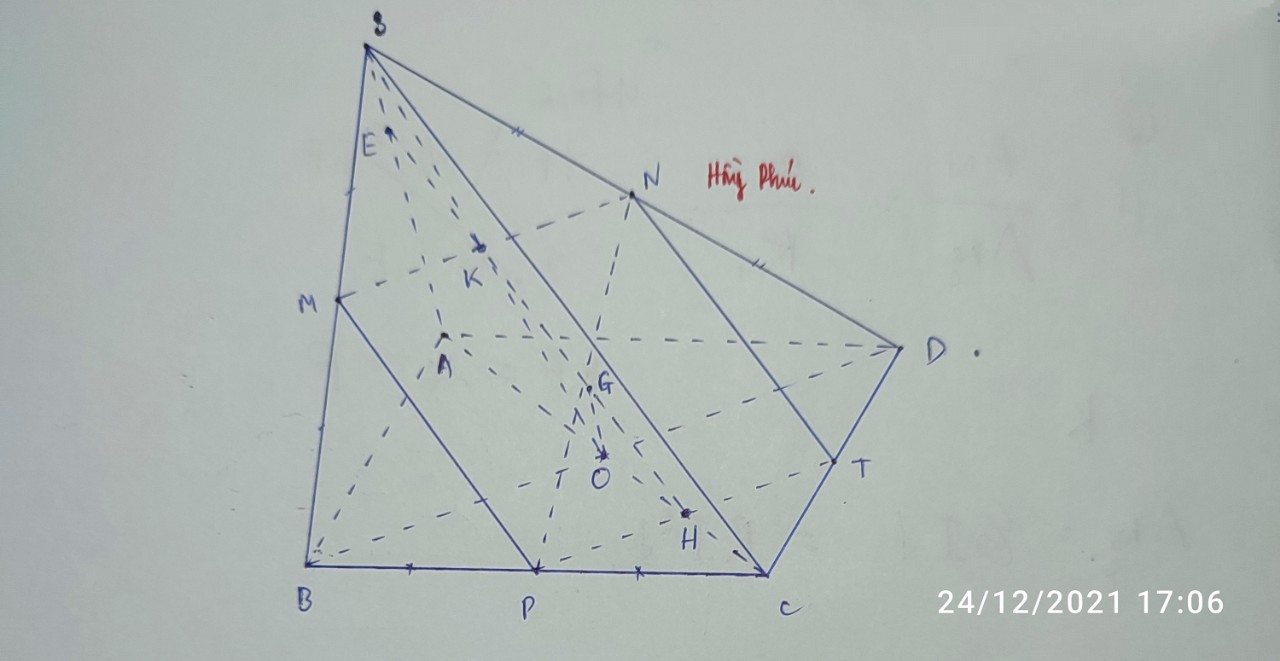
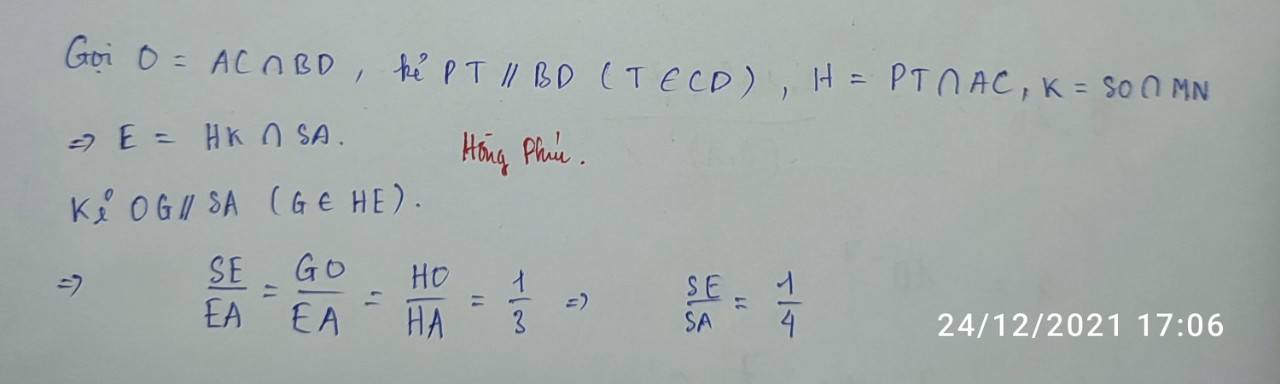
Chọn đáp án C.
là đường thẳng đi qua M, song song với AC và cắt BC tại trung điểm N của cạnh BC.
Gọi h là độ dài chiều cao của hình hộp đã cho. Khi đó: