Số
Trong hình bên:
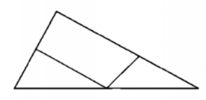
a) Có ... hình tam giác
b) Có ... hình tứ giác
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 2 2023
a: \(AB=\sqrt{\left(2+1\right)^2+\left(1-1\right)^2}=3\)
\(BC=\sqrt{\left(-1-2\right)^2+\left(-3-1\right)^2}=5\)
\(AC=\sqrt{\left(-1+1\right)^2+\left(-3-1\right)^2}=4\)
=>C=3+4+5=12
b: Tọa độ trọng tâm là:
\(\left\{{}\begin{matrix}x=\dfrac{-1+2-1}{3}=0\\y=\dfrac{1+1-3}{3}=-\dfrac{1}{3}\end{matrix}\right.\)
c: ABCD là hình bình hành
=>vecto AB=vecto DC
=>-1-x=2-(-1)=3 và -3-y=1-1=0
=>x=-4 và y=-3
I
3 tháng 2 2023
a) Ta có :
\(\overrightarrow{AB}=3\\ \overrightarrow{BC}=5\\ \overrightarrow{AC}=4\)
Chu vi tam giác là :
AB + BC + AC = 3 + 4 + 5 = 12
b) Toạ độ trọng tâm của tam giác ABC là :
\(\left(\dfrac{x_A+x_B+x_C}{3};\dfrac{y_A+y_B+y_C}{3}\right)=\left(\dfrac{-1+2+\left(-1\right)}{3};\dfrac{1+1+\left(-3\right)}{3}\right)=\left(0;-\dfrac{1}{3}\right)\)
c) Cho điểm D ( x ; y )
Để tứ giác ABCD là hình bình hành thì :
\(\overrightarrow{AD}=\overrightarrow{BC}\)
\(\Leftrightarrow\left(x+1;y-1\right)=\left(-3;-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}x=-4\\y=-3\end{matrix}\right.\)
Vậy với D ( -4 ; -3 ) thì tứ giác ABCD là hình bình hành
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 9
Olm chào em. Đây là toán nâng cao chuyên đề toán tổng tỉ ẩn tỉ. Cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:
Giải:
Tỉ số độ dài cạnh tam giác với độ dài cạnh tứ giác là:
4 : 3 = \(\frac43\)
Theo bài ra ta có sơ đồ:
Theo sơ đồ ta có:
Độ dài cạnh tam giác là: 10 : (4 - 3) x 4 = 40(cm)
Độ dài cạnh tứ giác là: 40 - 10 = 30(cm)
Đáp số:...
CM
9 tháng 1 2018
Gọi độ dài cạnh tam giác và cạnh tứ giác là a,b (cm) (a > b)
Cạnh của tam giác dài hơn cạnh của tứ giác là 10cm nên:
a – b = 10 cm => a = 10 + b
Chu vi tam giác bằng chu vi tứ giác nên:
a + a + a = 4 × b => 3 × a = 4 × b => 3 × (10 + b) = 4 × b => 30 + 3 × b = 4 × b => b = 30 cm
Suy ra a = 10 + 30 = 40 cm
Vậy độ dài cạnh tam giác là 40 cm và độ dài cạnh tứ giác là 30cm
Phương pháp giải:
- Đếm số hình tam giác hoặc tứ giác trong hình đã cho.
- Chú ý ghép hình và đếm đủ cho tới hết.
Lời giải chi tiết:
a) Có 3 hình tam giác (Hình 1; 3; 1 + 2 + 3).
b) Có 3 hình tứ giác (Hình 2; 1 + 2; 2 + 3).