Cho hình hộp chữ nhật . Vẽ một đường chéo của mặt ( ). Liệu đường chéo này có cắt các đường thẳng hay không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Hình hộp chữ nhật có:
A. 6 cạnh B. 10 cạnh
C. 8 cạnh D. 12 cạnh
Câu 2: Hình hộp chữ nhật có:
A. 4 mặt B.5 mặt
C. 6 mặt D. 8 mặt
Câu 3: Tính diện tích mặt đáy của hình hộp chữ nhật hình có chiều dài a, chiều rộng b , chiều cao h ( cùng đơn vị đo) được tính theo công thức:
A. S = a+bx2 C. S = a x b
B. (a+b)x2 D. a: b
Câu 4: Diện tích xung quanh của hình hộp chữ nhật là diện tích của:
A. 2 mặt đáy
B. 4 mặt xung quanh
C. 2 mặt xung quanh
D. 6 mặt
Câu 5: Chu vi mặt đáy của hình hộp chữ nhật có chiều dài 1,5dm, chiều rộng 1,2dm chiều cao 1dm là:
A. 5,4dm B. 2,5dm
C. 2,7dm D. 5 dm
Lời giải chi tiết: Chu vi mặt đáy là:
(1,5+1,2)×2=5,4(dm)
Đáp số: 5,4dm

a) Diện tích đáy hình hộp chữ nhật:
AB.AC=10.20=200(cm2)AB.AC=10.20=200(cm2)
Thể tích hình hộp chữ nhật:
V=S.h=200.15=3000(cm3)V=S.h=200.15=3000(cm3)
b) tam giác A'B'C' vuông tại B. Áp dụng định lý PITAGO ta có:
A′C′=√A′B′

a) Các đường thẳng vuông góc với BF là: AB, BC, CD, DA, AC, EF, FG, GH, HE và FH.
b) (ABCD) và (BCGF), (CDHG) và (EFGH), (ADHE) và (ABCD)
Lưu ý: HS có thể liệt kê tên các cặp mặt phẳng khác.
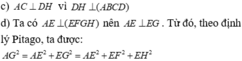

Đáp án B
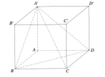
Giả độ dài các cạnh của khối hộp lần lượt là a; b; c khi đó T = 2ab + 2bc + 2ca = 36.
⇔ a b + b c + c a = 18 . Mặt khác A C ' = A B 2 + A D 2 + A A ' 2 = a 2 + b 2 + c 2 = 6
Khi đó a 2 + b 2 + c 2 = 36 a b + b c + c a = 18 ⇒ a + b + c 2 = 72 a b + b c + c a = 18 ⇔ a + b + c = 6 2 b a + c + a c = 18
Ta có: V = a b c = b . 18 - b a + c = b 18 - b 6 2 - b = b 3 - 6 2 b 2 + 18 b = f b
Xét f b = b 3 - 6 2 b 2 + 18 b , 0 < b < 6 2 ta có : f ' b = 3 b 2 - 12 2 b + 18 = 0 ⇔ b 2 - 4 b 2 + 6 = 0
⇔ [ b = 3 2 b = 3 ⇒ f 3 2 = 0 ; f 2 = 8 2 ⇒ M a x ( 0 ; 6 2 ) f b = 8 2 .

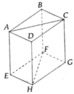


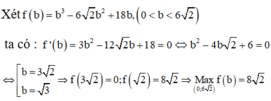
Kẻ đường chéo D C 1 .Đường chéo D C 1 cắt DC tại D
Vì mặt bên của hình hộp chữ nhật là một hình chữ nhật nên D C 1 cắt đường chéo C 1 D
Đường chéo D C 1 hay đường chéo D C 1 đều cắt cạnh D D 1 , C D , D 1 C , CD, D1C