OLM Class: Học trực tiếp cùng giáo viên OLM (hoàn toàn mới)!
🔥OLM: CHUẨN BỊ NĂM HỌC MỚI KHÔNG LO CHẬM NHỊP!
Tham gia chuỗi tập huấn Miễn Phí cho Giáo viên và Nhà trường 2025 từ OLM!
🔥 Lớp học thử cùng giáo viên OLM Class, HOÀN TOÀN MIỄN PHÍ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Cho ba số phức z 1 , z 2 , z 3 thỏa mãn
z 1 = z 2 = z 3 = 1 z 1 2 = z 2 . z 3 z 1 - z 2 = 6 + 2 2
Tính giá trị của biểu thức M = z 2 - z 3 - z 3 - z 1 .
A. - 6 - 2 - 3
B. - 6 - 2 + 3
C. 6 + 2 - 2 2
D. - 6 - 2 + 2 2
Đáp án D
Cách 1: Đại số
Từ (1) .
Thế vào (2) ta được: (3)
Từ (1) và (3): .
Cách 2: Hình học
Ta có:
(1)
Gọi M 1 , M 2 , M 3 là 3 điểm biểu diễn z 1 , z 2 , z 3
Dễ dàng có:
(2)
Từ (1) và (2):
Cách 3: Chuẩn hóa chọn z 1 = 1 .
Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?
Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a - b
Cho số phức z thỏa mãn \(z^6-z^5+z^4-z^3+z^2-z+1=0\)Tìm phần thực của \(w=z\left(z^2-z+1\right)\)
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
Số phức z thỏa mãn z^6-z^5+z^4-z^3+z^2-z+1=0. Tìm phần thực của w=z(z^2-z+1).
Số phức z thỏa mãn ( 2 + 3 i ) z + 1 - i z = 3 + 5 i Tìm môđun của số phức z.
A. 11
C. 9
Cho số phức z thỏa mãn z + ( 2 + i ) z ¯ = 3 + 5 i . Tính môđun của số phức z.
Đáp án C.
Cho N là điểm biểu diễn số phức z thỏa mãn \(\dfrac{z+2-3i}{z-3}=1-i\) và M là điểm biểu diễn số phức z' thoả mãn \(\left|z'-2-i\right|+\left|z'+3-3i\right|=\sqrt{29}\). Tìm giá trị nhỏ nhất của MN
Cho số phức thỏa mãn: z=a+bi, ( a , b ∈ R ) thỏa mãn: z ( 2 + i ) = z - 1 + i ( 2 z + 3 ) . Tính S = a + b
Cho số phức z thỏa mãn z - 2 i ≤ z - 4 i và z - 3 - 3 i = 1 . Giá trị lớn nhất của biểu thức P = z - 2 là:
A. 13 + 1
B. 10 + 1
C. 13
D. 10
Đáp án D
Cách 1: Đại số
Từ (1)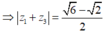 .
.
Thế vào (2) ta được: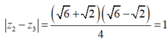 (3)
(3)
Từ (1) và (3):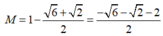 .
.
Cách 2: Hình học
Ta có:
Gọi M 1 , M 2 , M 3 là 3 điểm biểu diễn z 1 , z 2 , z 3
Dễ dàng có:
Từ (1) và (2):
Cách 3: Chuẩn hóa chọn z 1 = 1 .