Xét dấu của tam thức bậc hai sau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
7 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
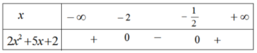
a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
PT
1
CM
24 tháng 9 2017
Tam thức 3 x 2 + x + 5 có biệt thức Δ = -59 < 0 và hệ số a = 3 > 0
Vậy 3 x 2 + x + 5 > 0, ∀x
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) Ta có \(a = - 2 < 0\), \(b = 4 = > b' = 2\) và \(c = - 5\)
\(\Delta ' = {2^2} - \left( { - 2} \right).\left( { - 5} \right) = - 6 < 0\)
=>\(f\left( x \right)\) cùng dấu âm với hệ số a.
=> \(f\left( x \right) < 0\forall x \in \mathbb{R}\)
b) Ta có: \(a = - 1,b = 6,c = - 9 = > b' = 3\)
\(\Delta ' = {3^2} - \left( { - 1} \right).\left( { - 9} \right) = 0\)
\(\frac{{ - b}}{{2a}} = \frac{{ - b'}}{a} = 3\)
=> \(f\left( x \right)\) cùng dấu âm với hệ số a với mọi \(x \in \mathbb{R}\backslash \left\{ 3 \right\}\)
=> \(f\left( x \right) < 0\forall x \in \mathbb{R}\backslash \left\{ 3 \right\}\)
23 tháng 9 2023
Tham khảo:
Tam thức bậc hai \(f\left( x \right) = - {x^2} - 2x + 8\) có hai nghiệm phân biệt \({x_1} = - 4,{x_2} = 2\) và hệ số \(a = - 1 < 0\).
Ta có bảng xét dấu \(f\left( x \right)\) như sau:
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
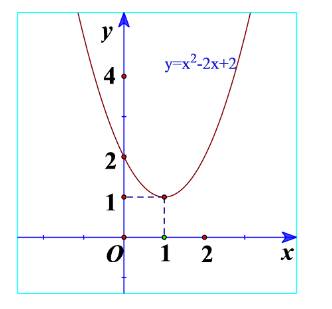
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
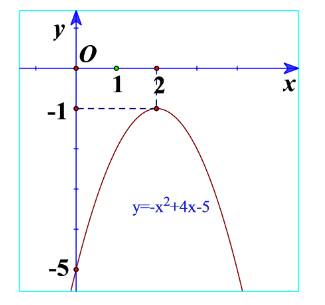
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 2{x^2} - 3x - 2\) có \(\Delta = 25 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{1}{2};{x_2} = 2\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
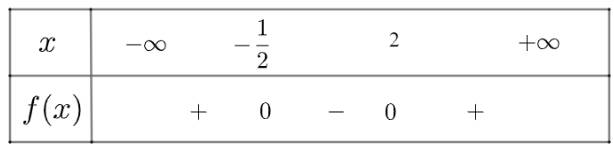
Vậy \(f\left( x \right)\) âm trong khoảng \(\left( { - \frac{1}{2},2} \right)\) và dương trong hai khoảng
\(\left( { - \infty , - \frac{1}{2}} \right)\) và \(\left( {2, + \infty } \right)\)
b) \(g\left( x \right) = - {x^2} + 2x - 3\) có \(\Delta = {2^2} - 4.\left( { - 1} \right).\left( { - 3} \right) = - 8 < 0\) và \(a = - 1 < 0\)
Vậy \(g\left( x \right)\)âm với mọi \(x \in \mathbb{R}\)
23 tháng 9 2023
Tham khảo:
a) Ta có tam thức bậc hai \(f\left( x \right) = {x^2} - x - 2\) có 2 nghiệm phân biệt \({x_1} = - 1,{x_2} = 2\) và hệ số \(a = 1 > 0\)
Ta có bảng xét dấu f(x) như sau:
Vậy tập nghiệm của bất phương trình là \(\left( { - \infty ; - 1} \right) \cup \left( {2; + \infty } \right)\)b) Từ bảng xét dấu ta thấy \(f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x < - 1\\x > 2\end{array} \right.\)
17 tháng 2 2022
b: \(\Delta=2^2-4\cdot1\cdot1=0\)
Do đó: Tam thức này dương khi x khác -1; bằng 0 khi x=-1
a: \(\Delta=3^2-4\cdot\left(-5\right)\cdot\left(-1\right)=9-20=-11< 0\)
Do đó: Tam thức này luôn âm với mọi x
c: \(\Delta=1^2-4\cdot1\cdot\left(-2\right)=9\)
Do đó: Tam thức này âm khi -2<x<1
Bằng 0 khi x=-2 hoặc x=1
Dương khi x<-2 hoặc x>1
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
a) \(f(x) = - 3{x^2} + x - \sqrt 2 \)có \(\Delta = 1 - 12\sqrt 2 < 0\)và a=-3<0 nên \(f(x) < 0\)với mọi \(x \in \mathbb{R}\)
b) \(g(x) = {x^2} + 8x + 16\) có \(\Delta = 0\)và a=1>0 nên g(x) có nghiệm kép \(x = - 4\) và g(x) >0 với mọi \(x \ne - 4\)
c) \(h(x) = - 2{x^2} + 7x - 3\) có \(\Delta = 25\)>0 và a=-2<0 và có 2 nghiệm phân biệt \({x_1} = \frac{1}{2};{x_2} = 3\)
Do đó ta có bảng xét dấu h(x)
Suy ra h(x) <0 với mọi \(x \in \left( { - \infty ;\frac{1}{2}} \right) \cup \left( {3; + \infty } \right)\) và h(x)>0 với mọi \(x \in \left( {\frac{1}{2};3} \right)\)