Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Để giải phương trình $x^2 - 6y^2 = 1$ với $x, y$ là số nguyên tố, ta sử dụng phương pháp giải bằng phương pháp Pell như sau: Phương trình có dạng $x^2 - 6y^2 = 1$, tương đương với phương trình $x^2 - 6y^2 - 1 = 0$. Ta cần tìm nghiệm nguyên của phương trình này, có dạng $(x, y)$. Giả sử $x_1, y_1$ là một nghiệm của phương trình, ta có thể tìm được một nghiệm khác bằng cách sử dụng công thức sau: $x_{n+1} = 5x_n + 12y_n$ $y_{n+1} = 2x_n + 5y_n$ Với $x_1 = 7, y_1 = 2$, ta có thể tìm được các giá trị $x$ và $y$ bằng cách lần lượt tính các giá trị $x_n$ và $y_n$ bằng công thức trên. $x_1 = 7, y_1 = 2$ $x_2 = 47, y_2 = 14$ $x_3 = 337, y_3 = 100$ $x_4 = 2387, y_4 = 710$ $x_5 = 16807, y_5 = 3982$ Vậy $(x, y) = (16807, 3982)$ là một nghiệm của phương trình $x^2 - 6y^2 = 1$, với $x$ và $y$ đều là số nguyên tố.
Lời giải:
$(x-1)(x+1)=6y^2$
$\Leftrightarrow x^2-1=6y^2$
$\Rightarrow x^2=6y^2+1$ lẻ $\Rightarrow x$ lẻ.
Ta biết 1 scp khi chia cho 4 thì dư $0$ hoặc $1$. Vì $x$ là số lẻ nên $x^2$ là scp lẻ $\Rightarrow$ $x^2$ chia $4$ dư $1$
$\Rightarrow 6y^2=x^2-1\vdots 4$
$\Rightarrow y^2\vdots 2$
$\Rightarrow y$ chẵn. Mà $y$ là số nguyên tố nên $y=2$.
Khi đó $x^2=6y^2+1=6.2^2+1=25$
$\Rightarrow x=5$ (thỏa mãn)
$
Sorry bạn nhưng mình từng giải bài này
Ta có phương trình đơn giản lại tương tự phương trình Pell như sau: $x^2 - 6y^2 = -1$ Ta có thể giải phương trình này bằng phương pháp Pell như sau: Giả sử $x_1, y_1$ là một nghiệm của phương trình, ta có thể tìm được một nghiệm khác bằng cách sử dụng công thức sau: $x_{n+1} = 5x_n + 12y_n$ $y_{n+1} = 2x_n + 5y_n$ Với $x_1 = 5, y_1 = 1$, ta có thể tìm được các giá trị $x$ và $y$ bằng cách lần lượt tính các giá trị $x_n$ và $y_n$ bằng công thức trên cho đến khi tìm được một nghiệm thỏa mãn $x^2 - 6y^2 = -1$. $x_1 = 5, y_1 = 1$ $x_2 = 29, y_2 = 5$ $x_3 = 169, y_3 = 29$ $x_4 = 985, y_4 = 169$ $x_5 = 5741, y_5 = 985$ Vậy $(x, y) = (5741, 985)$ là một nghiệm của phương trình $x^2 - 6y^2 = -1$. Ta kiểm tra xem $x$ và $y$ có phải đều là số nguyên tố hay không. Ta nhận thấy rằng $x$ chia hết cho 7, do đó $x$ không phải là số nguyên tố. Tuy nhiên, ta thấy rằng $y$ là số nguyên tố. Vì vậy, đáp án của bài toán là $(x, y) = (5741, 985)$ với $y$ là số nguyên tố.
2xy-6y+x=9
=>2yx-3.2y+x=9
=>2y.(x-3)+x=9
=>2y.(x-3)+(x-3)=9-3
=>(x-3).(2y+1)=6
=>x-3 ;2y+1 \(\in\)Ư(6)
Ư(6)={1 ;-1 ;2 ;-2 ;3 ;-3 ;6 ;-6}
Ta có bảng giá trị
x-3 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
2y+1 | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
2y | 5 | -7 | 2 | -4 | 1 | -3 | 0 | -2 |
y | \ | \ | 1\(\in Z\) | -2\(\in Z\) | \ | \ | 0\(\in Z\) | -1\(\in Z\) |
x | \ | \ | 5\(\in Z\) | 1\(\in Z\) | \ | \ | 9\(\in Z\) | -3\(\in Z\) |
Thử lại các đáp án đều đúng
Vậy (x,y) \(\in\){(5,1) ;(1,-2) ;(9,0),(-3,-1)}
Lời giải:
$|x|-|y|=60$
$|6y|-|y|=60$
$5|y|=60$
$|y|=12$
$\Rightarrow y=\pm 12$
$\Rightarrow x=6y=\pm 72$
Vậy $(x,y)=(72, 12), (-72, -12)$
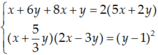
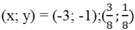
Theo giả thiết ta có x + 6 y + 8 x + y = 2 5 x + 2 y x − 1 x − 3 y = y + 2 2
⇔ x = 3 y 3 y − 1 3 y − 3 y = y + 2 2 ⇔ x = 3 y 0 = y + 2 2 ⇔ x = − 6 y = − 2 .
Suy ra x 2 + y 2 = 40.
Chọn đáp án A.