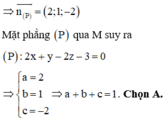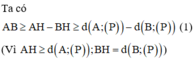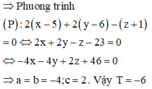Trong không gian với hệ trục tọa độ Oxyz, mặt phẳng đi qua hai điểm và cách một khoảng lớn nhất. Khi đó giá trị của biểu thức là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


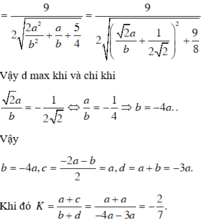

Đáp án B
Phương pháp:
- Đưa phương trình mặt phẳng (P) về dạng chỉ còn 1 tham số.
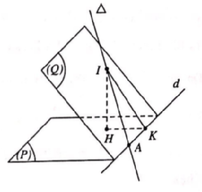
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất ó d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Cách giải:
![]()
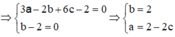
![]()
![]()
có tâm I(1;2;3) và bán kính R = 5
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Ta có
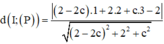
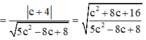
Ta tìm giá trị lớn nhất của 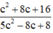 . Gọi m là giá trị của
. Gọi m là giá trị của 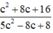 với c nào đó.
với c nào đó.
Ta có:
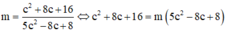
![]()
![]()
![]()
![]()
(*) có nghiệm ![]()
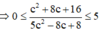
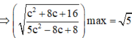
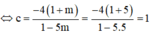
Khi đó ![]()

Đáp án B
Phương pháp:
- Đưa phương trình mặt phẳng (P) về dạng chỉ còn 1 tham số.
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S).
Cách giải:
![]()

![]()
( S ) : x - 1 2 + y - 2 2 + z - 3 2 = 25 có tâm I(1;2;3) và bán kính R = 5
- (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất <=> d(I;(P)) max, trong đó: I là tâm mặt cầu (S)
Ta có
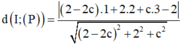
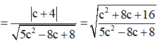
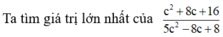
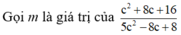
Ta có:
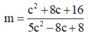
![]()
![]()
![]()
![]()
![]()
(*) có nghiệm
![]()
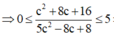
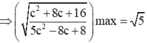
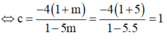
Khi đó T =a+b+c =2-2c+2+c=4-1 =3

Chọn C.
Phương pháp: Lập hệ phương trình tìm a,b,c.
Cách giải: Từ giả thiết ta có hệ:
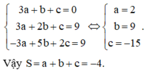

Đáp án A.
Ta có S : x + a 2 2 + y + b 2 2 + z + c 2 2 = a 2 + b 2 + c 2 4 - d có I - a 2 ; - b 2 ; - c 2
Vì I ∈ d ⇒ I 5 + t ; - 2 - 4 t ; - 1 - 4 t và (S) tiếp xúc với (P) nên d I ; P = R
3 . 5 + t - - 2 - 4 t - 3 . - 1 - 4 t - 1 3 2 + - 1 2 + - 3 2 = 19 ⇔ t + 1 = 1 ⇔ [ t = 0 t = 2
⇒ [ I ( 5 ; - 2 ; - 1 ) I ( 3 ; 6 ; 7 ) ⇒ [ a , b , c , d = - 10 ; 4 ; 2 ; 47 a , b , c , d = - 6 ; - 12 ; - 14 ; 75
Thử lại với a 2 + b 2 + c 2 4 - d = R 2 = 19 thì chỉ có trường hợp {-6;-12;-14;75} thỏa