Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
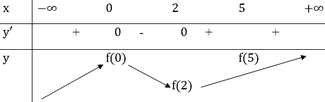
Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
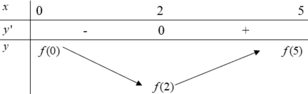
Suy ra 
Và 
Ta có 
Vì f(x) đồng biến trên đoạn [2;5] nên 
⇒ f(5)>f(0)
Vậy
Chọn đáp án D.
Đáp án C
Xét trên 0 , π ta có y ' = 1 - 2 sin x ⇒ y ' = 0 ⇔ sin x = 1 2 ⇔ x = π 4 ta có BBT như sau
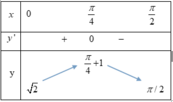
Như vậy GTLN của hàm số là π 4 + 1
Chọn B
Vì y = a x 3 + c x + d , a ≠ 0 là hàm số bậc ba và có m i n x ∈ - ∞ ; 0 f ( x ) = f ( - 2 ) nên a < 0 và y' = 0 có hai nghiệm phân biệt.
Ta có 
có hai nghiệm phân biệt
⇔
ac < 0
Vậy với a < 0, c > 0 thì y' = 0 có hai nghiệm đối nhau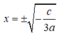 
Từ đó suy ra
⇔
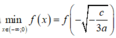
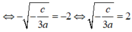
c = -12a
Ta có bảng biến thiên
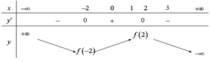
Ta suy ra 
Chọn A
Từ đồ thị của hàm số y = f'(x) ta có bảng biến thiên của hàm số y = f(x) trên đoạn [-1;2] như sau
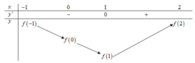
Nhận thấy
Để tìm 
ta so sánh f(-1) và f(2)
Theo giả thiết, 
Từ bảng biến thiên , ta có f(0) - f(1) > 0. Do đó f(2) - f(-1) > 0 
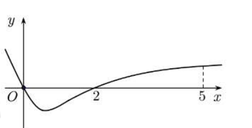
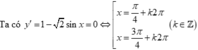
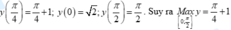
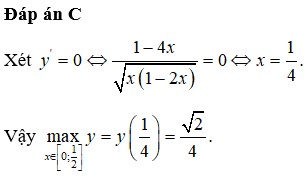
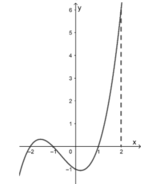
Vậy GTLN của hàm số trên [0; 3] là 250 27 đạt được khi x = 5/6. Chọn đáp án C.