Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
b) ta có: f(2) = 2 - 3 = -1
f(5) = 5 - 3 = 2
f(-1/2) = -1/2 - 3 = -7/2
ko bít đúng ko?? 565464654654654765876546266456456456756756757
a,y = f(x) = x - 3 nếu x =3 hoặc x > 3 và = -(x - 3) nếu x < 3
b,+ Với f(2), ta có: 2 < 3
-> y = f(2) = -(2 - 3) = -(-1) = 1
+ Với f(5), ta có: 5 > 3
-> y = f(5) = 5 - 3 = 2
+ Với f(\(-\frac{1}{2}\)), ta có: \(-\frac{1}{2}\)< 3
-> y = f(\(-\frac{1}{2}\)) = -(\(-\frac{1}{2}\)- 3) = -(\(-3\frac{1}{2}\)) = \(3\frac{1}{2}\)
c, Với f(x) = \(\frac{1}{3}\), ta có:
TH1: x > 3
Ta có:y = f(x) = x - 3 = \(\frac{1}{3}\)
-> x = \(\frac{1}{3}\)+ 3 =
Ta cod \(\hept{\begin{cases}f\left(x\right)>1\\f\left(x\right)=\frac{x+3}{x-2}\end{cases}}\)
<=> \(\frac{x+3}{x-2}>1\)
<=> \(\frac{x+3}{x-2}-1>0\)
\(\Leftrightarrow\frac{x+3-x-2}{x-2}>0\)
\(\Leftrightarrow\frac{1}{x-2}>0\)
<=> x - 2 > 0
<=> x = 2
Vậy x = 2
@@ Học tốt
Takigawa Miraii
Trả lời:
Ta có:\(f\left(x\right)=\frac{x+3}{x-2}\) \(\left(Đk:x\ne2\right)\)
Để\(f\left(x\right)>1\)
\(\Leftrightarrow\frac{x+3}{x-2}>1\)
\(\Leftrightarrow\frac{x+3}{x-2}-1>0\)
\(\Leftrightarrow\frac{x+3-x+2}{x-2}>0\)
\(\Leftrightarrow\frac{5}{x-2}>0\)
\(\Leftrightarrow x-2>0\)
\(\Leftrightarrow x>2\)(Thỏa mãn Đk: \(x\ne2\))
Vậy\(x>2\)thì hàm số\(f\left(x\right)=\frac{x+3}{x-2}>1\)
Hok tốt!
Good girl
a) * f(-2)
=-2.(-2)+1
=2
* f(3)
=-2.3+1
=-5
b) hàm số y=-2x+1
với x=-1 thì y=3 không bằng 1
Vậy M(-1,1)ko thuộc đồ thị hàm số f(x)
c) ta có 1>0
=> -2x+1=1
-2x=1-1
-2x=0
x=0/(-2)
x=0
=> x=0
vậy x=0 thì f(x)>0
nhớ k giùm mình nha
a)\(F\left(-2\right)=-2.\left(-2\right)+1=5\)
\(F\left(\frac{1}{2}\right)=-2.\left(\frac{1}{2}\right)+1=0\)
\(F\left(3\right)=-2.3+1=-5\)
\(F\left(1\right)=-2.1+1=-1\)
2: ĐKXĐ: x<>1
\(f'\left(x\right)=\dfrac{\left(x^2-3x+3\right)'\left(x-1\right)-\left(x^2-3x+3\right)\left(x-1\right)'}{\left(x-1\right)^2}\)
\(=\dfrac{\left(2x-3\right)\left(x-1\right)-\left(x^2-3x+3\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2-5x+3-x^2+3x-3}{\left(x-1\right)^2}=\dfrac{x^2-2x}{\left(x-1\right)^2}\)
f'(x)=0
=>x^2-2x=0
=>x(x-2)=0
=>\(\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
1:
\(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}\cdot x^2+8x-1\)
=>\(f'\left(x\right)=\dfrac{1}{3}\cdot3x^2-2\sqrt{2}\cdot2x+8=x^2-4\sqrt{2}\cdot x+8=\left(x-2\sqrt{2}\right)^2\)
f'(x)=0
=>\(\left(x-2\sqrt{2}\right)^2=0\)
=>\(x-2\sqrt{2}=0\)
=>\(x=2\sqrt{2}\)
Ta có f (-3/2) = 1 - 2.(-3/2) = 1 - (-3) = 4
f (3/2) = 1 - 2.(3/2) = 1 - 3 = -2
Vậy f (-3/2) > f (3/2)
Bài này dễ thôi bạn ak!hihi
- Ta có:f(-3/2)=1-2.(-3/2)
=1-(-3)=4
- f(3/2)=1-2.(3/2)
=1-3
=-2
Vậy :f(-3/2)>f(3/2)
//////Hihi!
Chọn A.
Với x = 1 ta có f(1) = k2
Với x ≠ 1 ta có
suy ra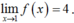
.
Vậy để hàm số gián đoạn tại x = 1 khi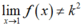
⇔ k2 ≠ 4 ⇔ k ≠ ±2.