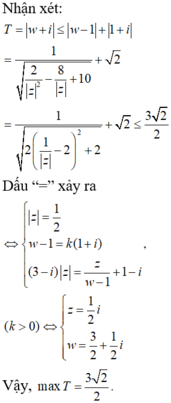Cho các số phức z 1 = 1 , z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i z − 3 ...

PT

Pham Trong Bach

14 tháng 8 2017

Cho các số phức z 1 = 1 , z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

14 tháng 8 2017

Đúng(0)

AS

An Sơ Hạ

17 tháng 4 2021

Câu 1 : Cho số phức \(z\) thỏa mãn \(z\) + ( 2 - i )\(\overline{z}\) = 3 - 5i. Môđun của số phức w = \(z \) - i bằng bao nhiêu ?Câu 2 : Cho số phức \(z\) = a + bi, (a,b ∈ R ) thỏa mãn ( 3 + 2i )\(z\) + ( 2 - i )2 = 4 + i. Tính P = a -...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

N

Ngann555

20 tháng 4 2021

undefined

Đúng(0)

PT

Pham Trong Bach

6 tháng 11 2018

Cho các số phức z 1 = 1, z 2 = 2 − 3 i và các số z thỏa mãn z − 1 − i + z − 3 + i = 2 2 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 11 2018

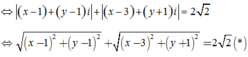
Đáp án B.

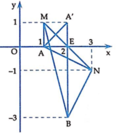
Số phức z 1 = 1 có điểm biểu diễn là A 1 ; 0 , số phức z 2 = 2 − 3 i có điểm biểu diễn là B 2 ; − 3

Gọi E x ; y là điểm biểu diễn của số phức z, khi đó z = x + y i , x , y ∈ ℝ

Suy ra

P = x − 1 + y i + x − 2 + y + 3 i = x − 1 2 + y 2 + x − 2 2 + y + 3 2

⇒ P = E A + E B .

Mặt khác

z − 1 − i + z − 3 + i = 2 2 ⇔ x − 1 + y − 1 i + x − 3 + y + 1 i = 2 2

⇔ x − 1 2 + y − 1 2 + x − 3 2 + y + 1 2 = 2 2 *

Gọi M 1 ; 1 , N 3 ; − 1 thì E M + E N = 2 2 = M N ⇒ Điểm E thuộc đoạn MN.

Ta có phương trình đường thẳng MN là x + y + z − 2 = 0 với x ∈ 1 ; 3

Bài toán trở thành:

Cho điểm E thuộc đoạn MN . Tìm giá trị lớn nhất của biểu thức P = E A + E B

Đặt f ( x ) = x + y − 2. Ta có

f 1 ; 0 = 1 + 0 − 2 = − 1 f 2 ; − 3 = 2 − 3 − 2 = − 3 ⇒ f 1 ; 0 . f 2 ; − 3 = 3 > 0 . Suy ra hai điểm A,B nằm cùng về một phía đối với MN . Gọi A' là điểm đối xứng với A qua MN thì A ' 2 ; 1 .Khi đó

P = E A + E B = E A ' + E B ≥ A ' B = 4 .

Dấu = xảy ra khi và chỉ khi

E ∈ A ' B ⇒ E = A ' B ∩ M N ⇒ E 2 ; 0 hay z = 2.

Do điểm E luôn thuộc đường thẳng MN nên P = E A + E B đạt giá trị lớn nhất khi E ≡ M hoặc E ≡ N .

Có

M A + M B = 1 + 17 N A + N B = 2 5 ⇒ M A + M B > N A + N B ⇒ max P = M A + M B...

Đúng(0)

PT

Pham Trong Bach

31 tháng 7 2018

Xét các số phức z thỏa mãn z + 1 - i + z - 3 + i = 2 5 . Tìm giá trị nhỏ nhất của P = z + 2 + 4 ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

31 tháng 7 2018

Đúng(0)

PT

Pham Trong Bach

24 tháng 3 2017

Cho các số phức z và w thỏa mãn ( 3 - i ) | z | = z w - 1 + 1 - i . Tìm GTLN của T = | w + i | ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

24 tháng 3 2017

Đáp án B.

Đúng(0)

PT

Pham Trong Bach

18 tháng 11 2018

Cho các số phức z và w thỏa mãn ( 3 - i ) z = z w - 1 + 1 - i . Tìm GTLN của T = w + i . A. 2 2 B. ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

18 tháng 11 2018

Đúng(0)

PT

Pham Trong Bach

12 tháng 4 2019

Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ ...

Đọc tiếp

#Hỏi cộng đồng OLM #Mẫu giáo

1

CM

Cao Minh Tâm

12 tháng 4 2019

Đúng(0)

PT

Pham Trong Bach

5 tháng 10 2017

Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ . ...

Đọc tiếp

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

5 tháng 10 2017

Đúng(0)

PT

Pham Trong Bach

30 tháng 5 2019

Các số phức z, w thay đổi nhưng thỏa mãn |z + i – 2i| = 1 và |w - 3 + i| = 3. Tìm |z - w|_max

A. |z - w|max = 2.

B. |z - w|max = 4.

C. |z - w|max = 9.

D. |z - w|max = 10.

#Hỏi cộng đồng OLM #Toán lớp 12

1

CM

Cao Minh Tâm

30 tháng 5 2019

Đáp án C

Đúng(0)

A

AllesKlar

23 tháng 4 2022

Tìm tất cả các số phức \(z\) thỏa mãn điều kiện:

\(\left|iz-1-3i\right|.\left|\overline{z}+1+i\right|=\left|z^2+\left(-6+2i\right)z+8-6i\right|\) và \(\dfrac{z-3}{z+2}\) là số thuần ảo.

#Hỏi cộng đồng OLM #Toán lớp 12

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP