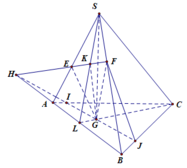
Cho tứ diện S. ABC. Lấy điểm E; F lần lượt trên đoạn SA; SB và điểm G trọng tâm giác ABC. Gọi H là giao điểm của EF và AB; J là giao điểm của HG và BC. Tìm giao tuyến của (EFG) và (SGC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 2 2017
Đúng(0)
Những câu hỏi liên quan
22 tháng 1 2020
SADE =360 x \(\frac{1}{2}\)x\(\frac{1}{2}\)=90 (cm2)
SDECB =360 - 90 = 270 (cm2)
13 tháng 4 2016
209 tôi tính dựa theo định luật bảo tàng động lương đó
ko bít giải đúng ko nhỉ
hay cậu bấm máy tính phương trình nghiệm: EQN(số 5 trong Model)
nhưng cậu phải lập hệ ms giải đc
11 tháng 1 2022
Diện tích tam giác ADE là:
\(\dfrac{1}{2}\times AD\times AE=\dfrac{1}{2}\times\dfrac{1}{3}AB\times\dfrac{1}{3}AC=\dfrac{1}{18}\times AB\times AC.\left(1\right)\)
Diện tích tam giác ABC là:
\(\dfrac{1}{2}\times AB\times AC.\left(2\right)\)
Từ \(\left(1\right)\left(2\right).\rightarrow\) Diện tích tam giác ABC = 9 lần diện tích tam giác ADE.
\(\rightarrow\) Diện tích tam giác ADE = \(72:9=8cm^2.\)
Diện tích tứ giác DECB = Diện tích tam giác ABC + Diện tích tam giác ADE \(\text{= 72 + 9 = 81 (cm2).}\)
Đáp số: 81 (cm2).
8 tháng 6 2018
Giải:
a) Diện tích tam giác ABC = 1/2 x AH x BC
Diện tích tam giác ABE = 1/2 x AH x BE
= 1/2 x AH x 2/3 BC
= 1/2 x AH x BC x 2/3
= Diện tích tam giác ABC x 2/3
Vậy: Diện tích tam giác ABE = 2/3 diện tích tam giác ABC.
b) Vì chiều cao DE có D là trung điểm nên Diện tích tam giác ABE = 2 lần diện tích tam giác BDE
= 12 x 2
= 24
Diện tích tam giác ABC = 24 : 2/3
= 36
c) Diện tích hình tứ giác ADEC là: 36 - 24 = 12 ( cm vuông)
Đáp số: ...........................