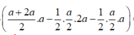Cho hình chóp S. ABCD có đáy là hình thang; đáy lớn AB. Gọi I; J; K lần lượt là 3 điểm trên SA; AB; BC. Gọi E là giao điểm của AK và BD. Tìm giao điểm của IK và (SBD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn D
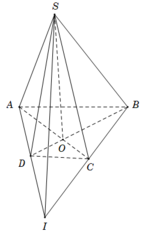
+Hình chóp S. ABCD có 4 mặt bên là (SAB); (SBC) ; (SCD) và (SAD): Do đó A đúng.
+ S là điểm chung thứ nhất của hai mặt phẳng (SAC) và (SBD)
là điểm chung thứ hai của hai mặt phẳng (SAC) và (SBD)
O ∈ A C ⊂ S A C ⇒ O ∈ S A C O ∈ B D ⊂ S B D ⇒ O ∈ S B D ⇒ O
=> giao tuyến của ( SAC) và (SBD) là SO.
Do đó B đúng.
+ Tương tự, ta có giao tuyến của mặt phẳng (SAD) và ( SBD) là SI ( I là giao điểm của AD và BC). Do đó C đúng.
+ giao tuyến của ( SAB) và (SAD) là SA mà SA không phải là đường trung bình của hình thang ABCD.
Do đó D sai.

Đáp án A

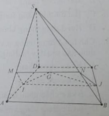
ABCD là hình thanh cân có AB = BC = CD = a; AD = 2a nên M là tâm của đáy ABCD.
SA = AD = 2a; SA ⊥ (ABCD) => tam giác SAD vuông cân tại A nên tâm mặt cầu ngoại tiếp hình chóp S.ABCD là trung điểm N của SD
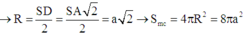

Do IJ là đường thẳng trung bình của hình thang ABCD nên IJ // AB. Hai mặt phẳng (GIJ) và (SAB) lần lượt chứa hai đường thẳng song song nên giao tuyến của chúng là đường thẳng đi qua G và song song với AB. Đường thẳng này cắt SA tại điểm M và cắt SB tại N. vậy thiết diện là hình thang MIJN, với M, N là giao điểm của đường thẳng đi qua G và song song với AB với hai đường thẳng SA, SB.
Đáp án B.

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\BC\perp AB\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\Delta SBC\) vuông tại B
b. \(\left\{{}\begin{matrix}SA\perp BD\\BD\perp SC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow BD\perp AC\)
\(\Rightarrow\widehat{BCA}=\widehat{ABD}\) (góc có cạnh tương ứng vuông góc)
\(\Rightarrow AD=AB.tan\widehat{ABD}=AB.\dfrac{AB}{BC}=\dfrac{a}{2}\)
c. Theo c/m câu a ta có \(BC\perp\left(SAB\right)\), mà \(AD||BC\Rightarrow AD\perp\left(SAB\right)\)
\(\Rightarrow AD\perp BM\)
Mà \(BM\perp DE\) (do DE là đường cao ứng với BM)
\(\Rightarrow BM\perp\left(ADE\right)\Rightarrow BM\perp AE\)
Áp dụng hệ thức lượng trong tam giác vuông ABM:
\(AE=\dfrac{AM.AB}{\sqrt{AM^2+AB^2}}=\dfrac{ax}{\sqrt{a^2+x^2}}\)
Pitago tam giác vuông ADE:
\(DE^2=AE^2+AD^2=\dfrac{a^2x^2}{a^2+x^2}+\dfrac{a^2}{4}\)
Do \(AD=\dfrac{a}{2}\) không đổi nên DE max, min tương ứng khi AE max, min
Hiển nhiên \(AE\ge0\Rightarrow AE_{min}=0\) khi \(x=0\) khi đó DE min
\(AE^2=\dfrac{a^2x^2}{a^2+x^2}\le\dfrac{a^2x^2}{2ax}=\dfrac{ax}{2}\le\dfrac{a^2}{2}\)
\(\Rightarrow AE_{max}\) khi \(x=3\)

Đáp ván A
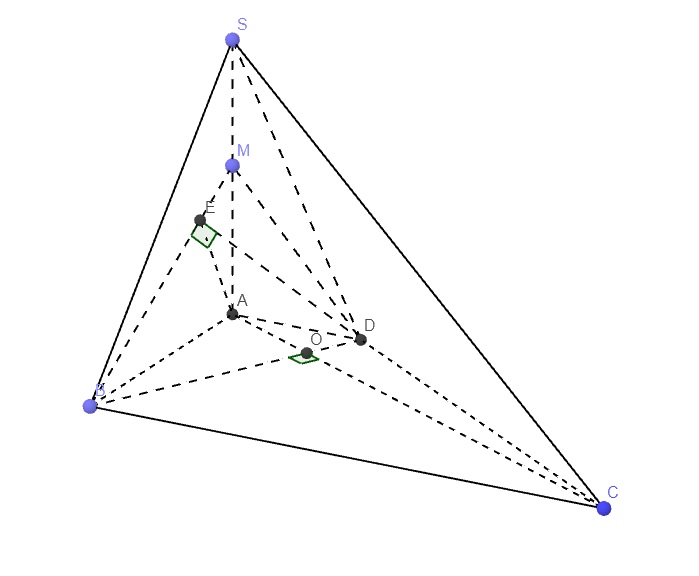
Vì I là hình chiếu của S trên (ABCD)
⇒ ( S C → , ( A B C D ) ) = S C I ⏞
⇒ S I = I C . tan 60 ° = a 5 2 . tan 60 ° = a 15 2
Vậy
V S . I B C = V S . A B C D - V S . A I B - V S . I C D = 1 3 . a 15 2 a + 2 a 2 . a - 1 2 . a 2 . 2 a - 1 2 . a 2 . a = a 3 15 8


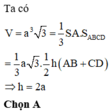
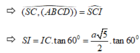 =
a
15
2
=
a
15
2