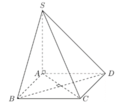
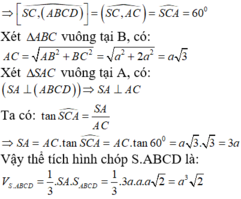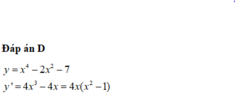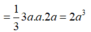Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB=a; . Mặt bên SAB là tam giác cân đỉnh S và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Biết . Góc giữa hai mặt phẳng (SAD) và (SBC) bằng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án D
Diện tích hình chữ nhật ABCD là S = 2a2, chiều cao SA =a.
Vậy thể tích khối chóp S.ABCD là V = 1 3 . 2 a 2 . a = 2 3 a 3

Đáp án B
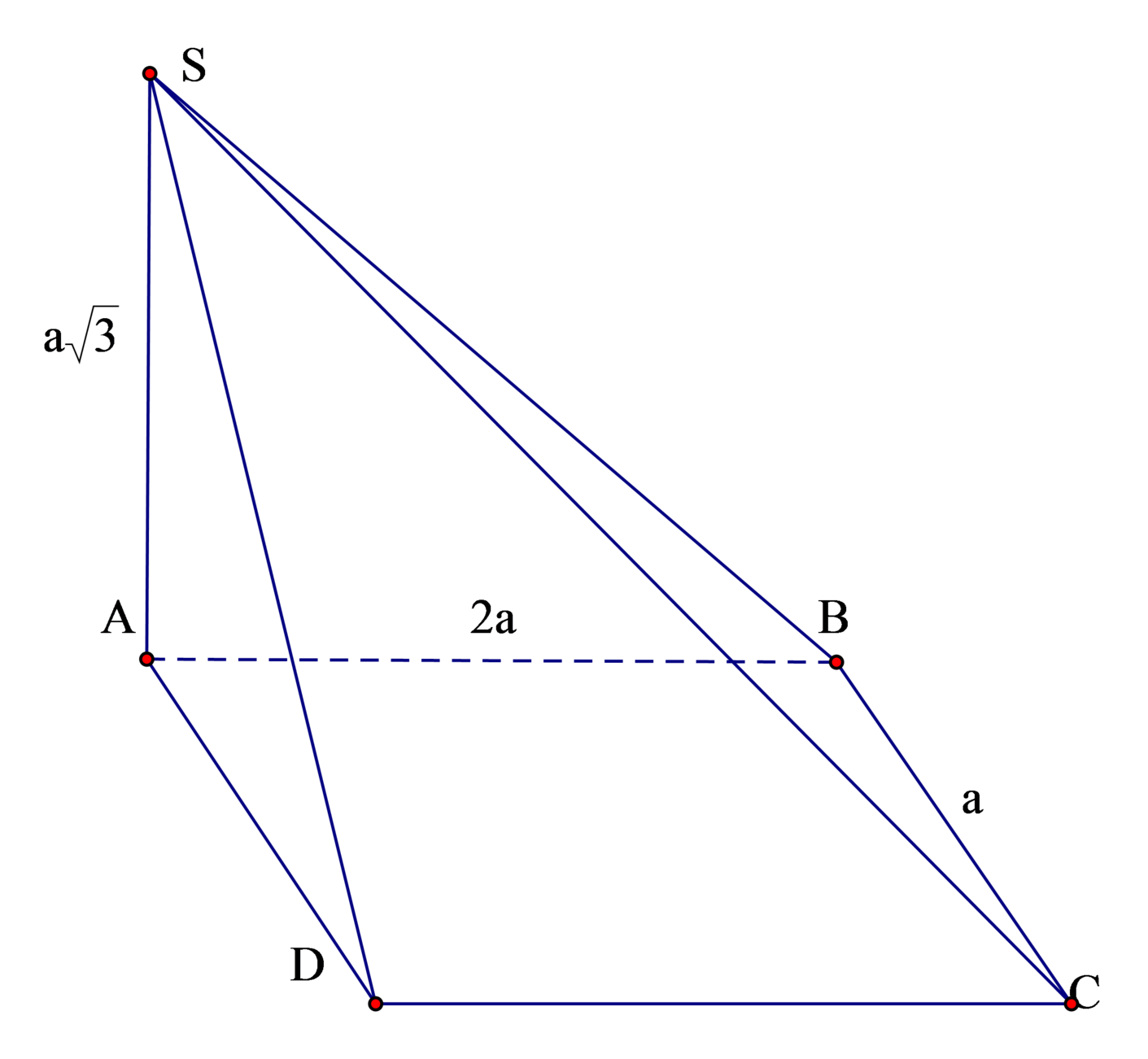
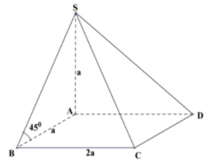
Do S A ⊥ A B C D
⇒ V S A B C D = 1 3 S A . d t A B C D = 1 3 S A . A B . B C = 1 3 a 3 .2 a . a = 2 a 3 3 3

Đáp án B
Thể tích khối chóp là
V = 1 3 S A . S A B C D = 1 3 . a . 3 .2 a . a = 2 a 3 3 3

Đáp án B
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3

Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).