x2-10x+y2-10y+74=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VD
3
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 8 2023
\(=\left(x-y\right)\left(x+y\right)-10\left(x+y\right)=\)
\(=\left(x+y\right)\left(x-y-10\right)\)
22 tháng 8 2023
= (x - y). (x + y) - 10 ( x - y)
= [( x + y) - 10)] . ( x - y)
NH
2
11 tháng 8 2021
a) Ta có: \(M=x^2-2xy+y^2-10x+10y\)
\(=\left(x-y\right)^2-10\left(x-y\right)\)
\(=9^2-10\cdot9=-9\)
26 tháng 3 2022
Ta có: \(4\ge2\left(x^2+y^2\right)\ge\left(x+y\right)^2\)
\(\Rightarrow x+y\le2\)
Ta có: \(P=\sqrt{x\left(14x+10y\right)}+\sqrt{y\left(14y+10x\right)}\)
\(=\sqrt{\dfrac{24x\left(14x+10y\right)}{24}}+\sqrt{\dfrac{24y\left(14y+10x\right)}{24}}\le\dfrac{\dfrac{24x+14x+10y}{2}}{\sqrt{24}}+\dfrac{\dfrac{24y+14y+10x}{2}}{\sqrt{24}}\)
\(\Leftrightarrow P\le\dfrac{24\left(x+y\right)}{2\sqrt{6}}\le\dfrac{24.2}{2\sqrt{6}}=4\sqrt{6}\)
Dấu "=" xảy ra ⇔ x = y = 1
CM
17 tháng 6 2017
Ta có hệ số a= 5; b= 0 và c= -11 nên bán kính là R= a 2 + b 2 - c = 6
Chọn A.
CM
11 tháng 1 2019
Đáp án: A
Ta có:
(C): x 2 + y 2 - 8x + 10y + 2m - 1 = 0 ⇔ (x - 4 ) 2 + (y + 5 ) 2 = 42 - 2m
Để (C) là phương trình đường tròn thì 42 - 2m > 0 ⇔ m < 21
CM
9 tháng 5 2017
Ta có: đường tròn: x2+ y2- 10x + 1= 0 => (x- 5)2 + y2= 24 có tâm I(5;0) .Khoảng cách từ I đến Oy là d ( I ; O y ) = 5
Chọn D.
CM
4 tháng 12 2017
Ta có hệ số a= 4; b= -5 và c= m.
Để C là đường tròn có bán kính R= 7 thì:
R = 4 2 + 5 2 - m = 7 ⇔ m = - 8
Chọn C.
CM
27 tháng 1 2019
Đáp án A.
Phương trình mặt cầu (S) có tâm O(a,b,c) bán kính R là:
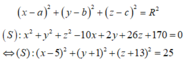
Suy ra tọa độ tâm mặt cầu là (5; -1; -13)
Lần sau bạn nhớ chú ý gõ đầy đủ yêu cầu đề. Các bạn muốn nhận sự trợ giúp mà đến đề bài còn không viết cho tử tế thì còn ai muốn giúp nữa?
Coi đây là bài toán tìm $x,y$.
Lời giải:
$x^2-10x+y^2-10y+74=0$
$\Leftrightarrow (x^2-10x+5^2)+(y^2-10y+5^2)+24=0$
$\Leftrightarrow (x-5)^2+(y-5)^2+24=0$
$\Leftrightarrow (x-5)^2+(y-5)^2=-24< 0$ (vô lý vì bình phương 1 số thực thì luôn không âm)
Do đó không tồn tại $x,y$ thỏa mãn đề bài.