tìm a,b biết rằng f(x) =x4+1.Chia hết cho đa thức x2+ax+b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 10 2017
Ta có
Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
ó (a – 1)x + b + 30 = 0 với mọi x
ó a - 1 = 0 b + 30 = 0 ó a = 1 b = - 30
Vậy a = 1; b = -30
Đáp án cần chọn là: D
CM
18 tháng 12 2017
Ta có
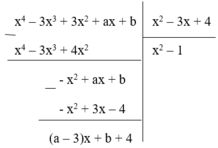
Phần dư của phép chia f(x) cho g(x) là R = (a – 3)x + b + 4. Để phép chia trên là phép chia hết thì R = 0, Ɐx
ó (a – 3)x + b + 4 = 0, Ɐx ó a - 3 = 0 b + 4 = 0
ó a = 3 b = - 4 => ab = -12
Đáp án cần chọn là: A
24 tháng 10 2021
\(f\left(x\right)⋮g\left(x\right)\)
\(\Leftrightarrow x^4-3x^3+4x^2-x^2+3x-4+\left(a-3\right)x+\left(b+4\right)⋮x^2-3x+4\)
\(\Leftrightarrow\left(a,b\right)=\left(3;-4\right)\)
2 tháng 9 2018
Đặt phép chia sau đo tính số dư
Vì x4+1 chia hết cho x2+ax +b ∀ x
⇒ số dư = 0 ⇒ từng cái = 0 ⇒ a= ; b =
NM
1
3 tháng 4 2020
\(x^4+1=x^4+ax^3+bx^2-ax^3-a^2x^2-abx-bx^2-abx-b^2+a^2x^2+2abx+b^2+1\)
\(=x^2\left(x^2+ax+b\right)-ax\left(x^2+ax+b\right)-b\left(x^2+ax+b\right)+a^2x^2+2abx+b^2+1\)
\(=\left(x^2-ax-b\right)\left(x^2+ax+b\right)+\left(ax+b\right)^2+1\)
Ta có : \(x^4+1⋮x^2+ax+b\Leftrightarrow\left(ax+b\right)^2+1=0\)( phần dư = 0 )
Mà \(\left(ax+b\right)^2+1\ge1>0\)
Vậy không có a,b thỏa mãn đề bài
29 tháng 5 2023
A(x)=(1-x^n)(1+x^n)/(1-x)(1+x)
B(x)=1-x^n/1-x
A(x) chia hết cho B(x) khi 1-x^n chia hết cho 1+x
x^n+1/x+1=A(x)+(1+(-1)^n)/(x+1)
=>1-x^n chia hết cho 1+x khi và chỉ khi n=2k+1
Đặt f(x)=\(\left(x^2+ax+b\right)\left(x^2+mx+n\right)\)
\(\Leftrightarrow\hept{\begin{cases}a=\sqrt{2}\\b=1\end{cases}}\)hoặc \(\hept{\begin{cases}a=-\sqrt{2}\\b=1\end{cases}}\)