Xét sự tính chẵn lẻ của hàm số y= x^2020-2x^2-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
Y
16 tháng 10 2023
\(TXD\) \(D=R\backslash\left\{0\right\}\) là tập đối xứng.
\(\forall x\in D\Rightarrow-x\in D\)
Có \(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|2\left(-x\right)+1\right|+\left|2\left(-x\right)-1\right|}\)
\(=\dfrac{x^2+1}{\left|1-2x\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|-\left(2x-1\right)\right|+\left|-\left(2x+1\right)\right|}\)
\(=\dfrac{x^2+1}{\left|2x-1\right|+\left|2x+1\right|}\) \(=f\left(x\right)\)
Vậy hàm số \(y=f\left(x\right)=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}\) là hàm số chẵn.
16 tháng 10 2023
TXĐ: D=R
Khi \(x\in D\) thì \(-x\in D\)
\(f\left(-x\right)=\dfrac{\left(-x\right)^2+1}{\left|-2x+1\right|+\left|-2x-1\right|}\)
\(=\dfrac{x^2+1}{\left|2x+1\right|+\left|2x-1\right|}=f\left(x\right)\)
=>f(x) chẵn
CM
25 tháng 8 2018
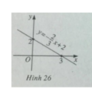
Đồ thị là hình 26. Hàm số không là hàm số chẵn, không là hàm số lẻ
CM
15 tháng 1 2017
Đáp án D
Ta có tập xác định D = R.
Hàm số y = f(x) = 0 có:
f(-x) = 0 và –f(x) = 0
=> f(x) = f(-x) = -f(x) vừa thỏa mãn tính chất của hàm số chẵn, vừa thỏa mãn tính chất của hàm số lẻ, nên đây là hàm số vừa chẵn vừa lẻ.
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Hàm số \(y = \sin 2x + \tan 2x\) có nghĩa khi \(tan 2x\) có nghĩa
\(\cos 2x \ne 0\;\; \Leftrightarrow 2x \ne \frac{\pi }{2}\;\;\;\; \Leftrightarrow x \ne \frac{\pi }{4} + \frac{{k\pi }}{2}\) \
Vây tập xác định của hàm số là \(D = \mathbb{R}\;\backslash \left\{ {\frac{\pi }{4} + \frac{{k\pi }}{2}} \right\}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - 2x} \right) + \tan \left( { - 2x} \right) = - \sin 2x - \tan 2x = - \left( {\sin 2x + \tan 2x} \right) = - f\left( x \right),\;\forall x \in D\).
Vậy \(y = \sin 2x + \tan 2x\) là hàm số lẻ
b) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \cos \left( { - x} \right) + {\sin ^2}\left( { - x} \right) = \cos x + {\sin ^2}x = f\left( x \right),\;\forall x \in D\)
Vậy \(y = \cos x + {\sin ^2}x\) là hàm số chẵn
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
c) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right)\cos \left( { - 2x} \right) = - \sin x.\cos 2x = - f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x\cos \;2x\) là hàm số lẻ
d) Tập xác định của hàm số là \(D = \mathbb{R}\)
Do đó, nếu x thuộc tập xác định D thì –x cũng thuộc tập xác định D
Ta có: \(f\left( { - x} \right) = \sin \left( { - x} \right) + \cos \left( { - x} \right) = - \sin x + \cos x \ne f\left( x \right),\;\forall x \in D\)
Vậy \(y = \sin x + \cos x\) không là hàm số chẵn cũng không là hàm số lẻ
24 tháng 10 2021
\(f\left(-x\right)=\sqrt[3]{-x+2}-\sqrt[3]{-x-2}\)
\(=-\left(\sqrt[3]{x-2}-\sqrt[3]{x+2}\right)\)
=f(x)
Vậy: f(x) là hàm số chẵn
HP
12 tháng 12 2020
a, \(y=f\left(x\right)=2x^2+1\)
\(f\left(-x\right)=2x^2+1=f\left(x\right)\Rightarrow\) Là hàm chẵn
b, \(y=f\left(x\right)=5x^3-2x\)
\(f\left(-x\right)=-5x^3+2x=-f\left(x\right)\Rightarrow\) Là hàm lẻ
c, \(y=f\left(x\right)=\sqrt{x-1}\)
ĐK: \(x\ge1\)
\(-f\left(x\right)=-\sqrt{x-1}\ne f\left(x\right)\Rightarrow\) Không phải là hàm số chẵn, lẻ
d, \(y=f\left(x\right)=5x^2-\dfrac{1}{x}\)
ĐK: \(x\ne0\)
\(f\left(-x\right)=5x^2+\dfrac{1}{x}\ne f\left(x\right)\)
\(-f\left(x\right)=-5x^2+\dfrac{1}{x}\ne f\left(-x\right)\)
\(\Rightarrow\) Không phải là hàm số chẵn, lẻ
23 tháng 10 2021
b: \(f\left(-x\right)=\dfrac{\left|-x+1\right|+\left|-x-1\right|}{\left|-x+1\right|-\left|-x-1\right|}\)
\(=\dfrac{\left|x-1\right|+\left|x+1\right|}{\left|x-1\right|-\left|x+1\right|}\)
=-f(x)
Vậy: f(x) là hàm số lẻ
\(f\left(-x\right)=\left(-x\right)^{2020}-2\cdot\left(-x\right)^2-3\)
\(=x^{2020}-2x^2-3\)
=f(x)
=> f(x) là hàm số chẵn