cho tam giác ABC có ba góc nhọn.Gọi O là trung điểm của BC.Gọi D là điểm đối xứng của A qua BC;E là điểm đối xứng của A qua O.Chứng minh ràng BCED là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 8 2017
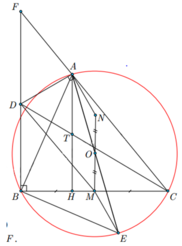
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .
23 tháng 8 2016
A B M F O K N C D
Có: BMNC là hình thang, KD là đường trung bình vì vậy:
\(KD=\frac{BM+NC}{2}\)
Lại có: \(\Delta AIO=\Delta DKO\) (cạnh góc vuông và góc nhọn kề) nên AI = DK.
Vậy: \(MB=CN=2DK=2AI\)
CH
Cô Hoàng Huyền
Admin
VIP
23 tháng 8 2016
???ng th?ng j: ???ng th?ng qua E, O ?o?n th?ng f: ?o?n th?ng [A, B] ?o?n th?ng g: ?o?n th?ng [B, C] ?o?n th?ng h: ?o?n th?ng [C, A] ?o?n th?ng i: ?o?n th?ng [A, D] ?o?n th?ng p: ?o?n th?ng [B, M] ?o?n th?ng q: ?o?n th?ng [A, F] ?o?n th?ng r: ?o?n th?ng [D, K] ?o?n th?ng s: ?o?n th?ng [N, C] A = (-0.99, 4.01) A = (-0.99, 4.01) A = (-0.99, 4.01) B = (-2.82, -1.84) B = (-2.82, -1.84) B = (-2.82, -1.84) C = 7.77 - 1.57? C = 7.77 - 1.57? C = 7.77 - 1.57? ?i?m D: Trung ?i?m c?a g ?i?m D: Trung ?i?m c?a g ?i?m D: Trung ?i?m c?a g ?i?m O: Trung ?i?m c?a A, D ?i?m O: Trung ?i?m c?a A, D ?i?m O: Trung ?i?m c?a A, D ?i?m M: Giao ?i?m c?a j, k ?i?m M: Giao ?i?m c?a j, k ?i?m M: Giao ?i?m c?a j, k ?i?m F: Giao ?i?m c?a j, m ?i?m F: Giao ?i?m c?a j, m ?i?m F: Giao ?i?m c?a j, m ?i?m K: Giao ?i?m c?a l, j ?i?m K: Giao ?i?m c?a l, j ?i?m K: Giao ?i?m c?a l, j ?i?m I: Giao ?i?m c?a j, m ?i?m I: Giao ?i?m c?a j, m ?i?m I: Giao ?i?m c?a j, m ?i?m N: Giao ?i?m c?a j, n ?i?m N: Giao ?i?m c?a j, n ?i?m N: Giao ?i?m c?a j, n
Thấy ngay BMNC là hình thang, KD là đường trung bình, vì thế nên : \(KD=\frac{BM+NC}{2}\)
Lại có: \(\Delta AIO=\Delta DKO\) (cạnh góc vuông và góc nhọn kề) nên AI = DK.
Vậy \(MB+CN=2DK=2AI.\)
15 tháng 7 2017
Xét tam giác COA tao có FD là đường trung bình
=> FD = 1/2 A'C'
chứng minh tương tự FD = 1/2 AC => A'C' =AC
chứng minh tương tự B'C"= BC; A'B'=AB
vậy tam giác ABC =tam giác A'B'C'
Xét tứ giác ACEB có:
AO = OE
BO = OC
=> Tứ giác ACEB là hình bình hành (DH)
=> AC // BE
Ta có: A đối xứng với E qua O thuộc BC; A lại đối xứng với D qua BC
=> ED // BC
=> Tứ giác BCDE là hình thang
Gọi giao của BC và AD là K
Xét tam giác ACD có: CK vừa là trung tuyến vừa là đường cao (GT)
=> Tam giác ACD là tam giác cân
=> CK cũng là tia phân giác góc C
=> Góc ACK = góc DCK
Lại có AC // BE (cmt)
=> Góc ACB = góc CBE
=> Góc DCB = góc EBC
=> Hình thang BCDE là hình thang cân (DH)