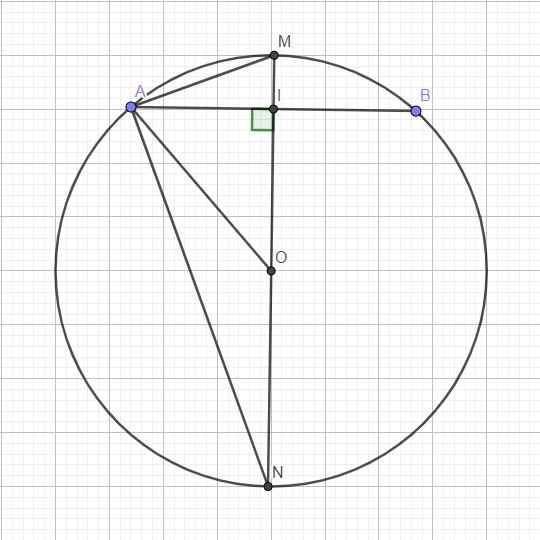
Cho AB là dây cung của (O;R) và I là trung điểm của AB (O không thuộc AB)
a) Chứng minh OI vuông góc AB
b) Qua I vẽ dây cung EF. Chứng minh EF>AB. Tìm độ dài lớn nhất, độ dài nhỏ nhất của các dây quay quanh I.
c) Cho R=5cm, OI=4cm, tính độ dài dây cung ngắn nhất qua I.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TT
Trần Thị Như Ý
1 tháng 9 2019
https://i.imgur.com/l9VOPy1.jpg
Đúng(0)
Những câu hỏi liên quan
15 tháng 10 2021
Xét ΔAMO vuông tại M có
\(OA^2=AM^2+OM^2\)
\(\Leftrightarrow AM=12\left(cm\right)\)
hay AB=24(cm)
20 tháng 2 2020
vẽ OK vuông góc với AB ta có AK=KB= \(\frac{R\sqrt{3}}{2}\)
áp dụng hệ thức lượng trong tam giác vuông KBO ta có :
\(sin\widehat{KOB}=\frac{KB}{OB}=\frac{\frac{\sqrt{3}}{2}R}{R}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{KOB}=60^0\)
Tương tự ta có :\(\widehat{AOK}=60^0\)
gọi sđ cung AnB là số đo cung AB nhỏ .
gọi sđ cung AmB là số đo cung AB lớn .
\(\Rightarrow\widehat{AOB}=120^0\Rightarrow sđAnB=120^0\)
mà \(sđAnB+sđAmB=360^0\)
\(\Rightarrow sđAmB=240^0\)
ta có \(\widehat{AMB}=\frac{sđAmB}{2}=\frac{240^0}{2}=120^0\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2024
Theo quan hệ giữa đường kính và dây cung, do \(OI\perp AB\) tại I \(\Rightarrow AI=BI\)
\(\Rightarrow OI\) là trung trực của AB hay OM là trung trực của AB
\(\Rightarrow MA=MB\)
\(\Rightarrow\stackrel\frown{MA}=\stackrel\frown{MB}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do I là trung điểm AB \(\Rightarrow OI\perp AB\)
\(AI=\dfrac{1}{2}AB=3\)
Trong tam giác vuông OAI, áp dụng Pitago:
\(OI=\sqrt{OA^2-AI^2}=\sqrt{R^2-AI^2}=4\)
\(\Rightarrow IM=OM-OI=R-OI=1\)
\(\Rightarrow AM=\sqrt{AI^2+IM^2}=\sqrt{10}\left(cm\right)\)
b.
Vẫn như trên, ta có: \(AI=\dfrac{1}{2}AB=6\)
Do MN là đường kính \(\Rightarrow\Delta MAN\) vuông tại A
Áp dụng hệ thức lượng trong tam giác vuông MAN với đường cao AI:
\(\dfrac{1}{AI^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\Rightarrow\dfrac{1}{6^2}=\dfrac{1}{10^2}+\dfrac{1}{AM^2}\Rightarrow AM=\dfrac{15}{2}\)
Áp dụng hệ thức lượng:
\(AI.MN=AN.AM\Leftrightarrow MN=\dfrac{AM.AN}{AI}=\dfrac{25}{2}\)
\(\Rightarrow R=\dfrac{MN}{2}=\dfrac{25}{4}\left(cm\right)\)
