Một hình nón có diện tích xung quanh 80π cm², diện tích đáy bằng 36π cm². Tính thể tích hình nón.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

AH
Akai Haruma
Giáo viên
23 tháng 6 2021
Lời giải:
Theo bài ra ta có:
$\pi rl=2\pi r^2$
$\Rightarrow l=2r=6$ (cm)
Mà theo định lý Pitago: $l^2=h^2+r^2$
$\Rightarrow h=\sqrt{l^2-r^2}=3\sqrt{3}$ (cm)
Thể tích hình nón:
$V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi. 3^2.3\sqrt{3}=9\sqrt{3}\pi$ (cm3)

1 tháng 4 2016
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
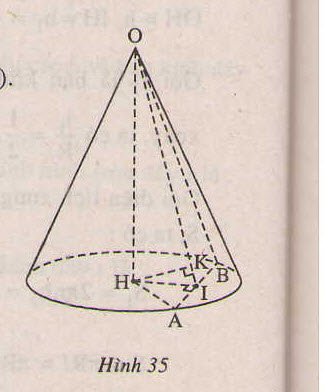
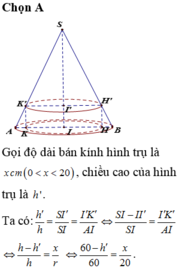

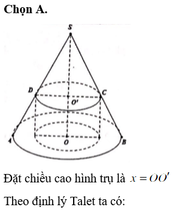



Lắp công thức tinh dịên h vào rồi giải hệ hai phương trình hai ân .\(S_{xq}=\pi rl=80\pi\)\(S_đ=\pi.r^2=\)36\(\pi\)Trong đó l đương sinh và r là ban kinh đay.Tìm được l,r rồi dùng Pitago tinh đường cao h .Lắp vào công thức tinh thể h là xong .