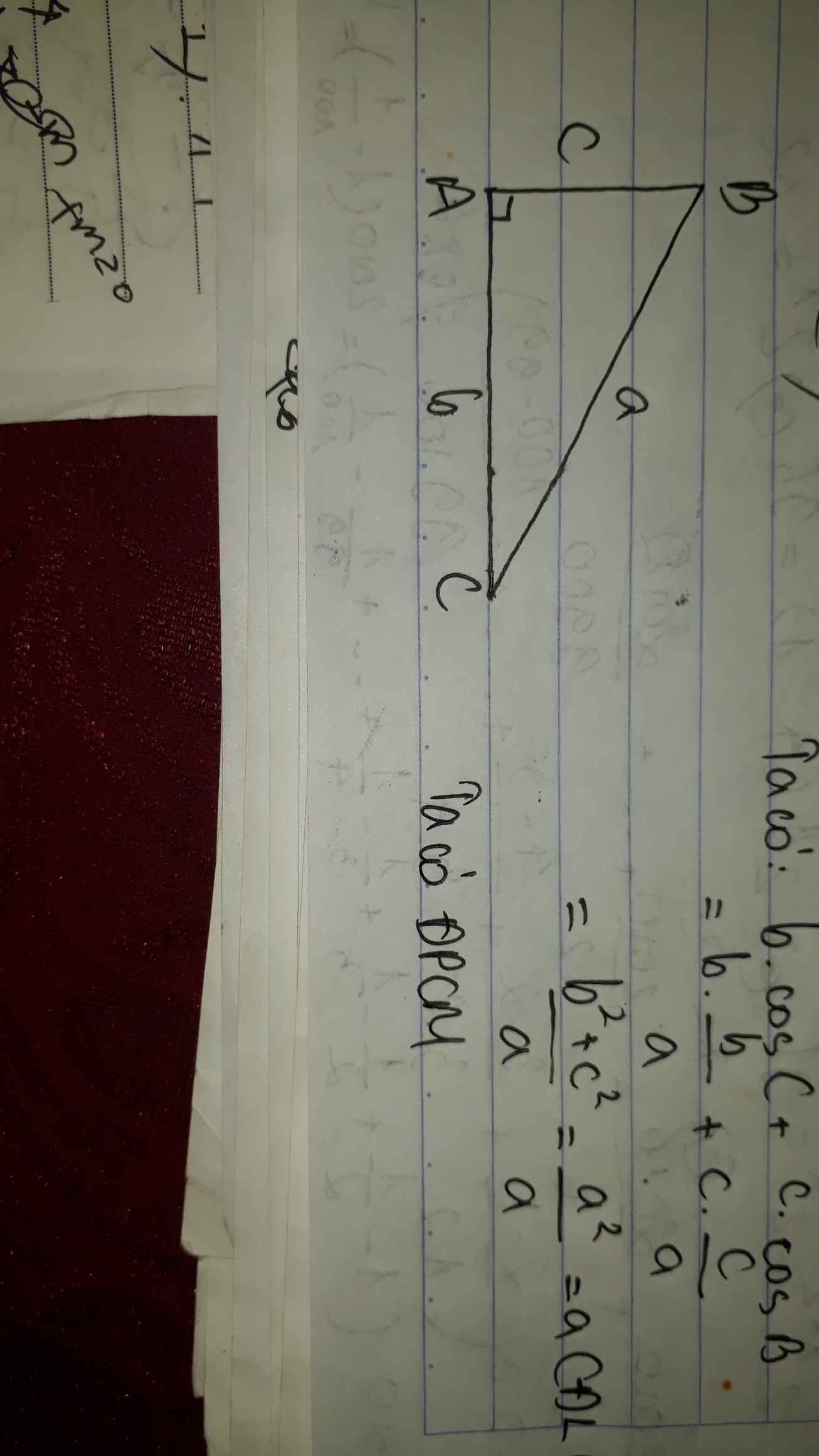chứng minh rằng tam giác ABC vuông nếu: cosB + cosC = \(\frac{b+c}{a}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
27 tháng 8 2019
a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
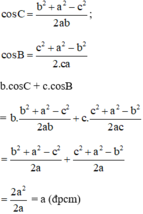
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 2 2021
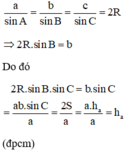
\(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
\(=\dfrac{b^2+c^2-a^2}{2abc}+\dfrac{a^2+c^2-b^2}{2abc}+\dfrac{a^2+b^2-c^2}{2abc}\)
\(=\dfrac{a^2+b^2+c^2}{2abc}\) (đpcm)
2 tháng 3 2021
a2 = b2 + c2 - 2bc.cosA
b2 = a2 + c2 - 2ac.cosB
c2 = a2 + b2 - 2ab.cosC
⇒ a2 + b2 + c2 = 2bc.cosA + 2ac.cosB + 2ab.cosC
⇒ VT = \(\dfrac{2bc.cosA}{2abc}+\dfrac{2ab.cosC}{2abc}+\dfrac{2ac.cosB}{2abc}\)
⇒ VT = \(\dfrac{cosA}{a}+\dfrac{cosB}{b}+\dfrac{cosC}{c}\)
14 tháng 7 2021
Áp dụng hệ quả của định lý Cosin ta có:
\(\cos C=\dfrac{b^2+a^2-c^2}{2ab};\cos B=\dfrac{c^2+a^2-b^2}{2ca}\)
\(\Rightarrow b\cos C+c\cos B=b\dfrac{b^2+a^2-c^2}{2ab}+c\dfrac{c^2+a^2-b^2}{2ca}=\)
\(\dfrac{b^2+a^2-c^2}{2a}+\dfrac{c^2+a^2-b^2}{2a}=\dfrac{2a^2}{2a}=a\)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 6 2020
\(cosA+cosB-cosC=2cos\frac{A+B}{2}.cos\frac{A-B}{2}+2sin^2\frac{C}{2}-1\)
\(=2sin\frac{C}{2}.cos\frac{A-B}{2}+2sin^2\frac{C}{2}-1\)
\(=2sin\frac{C}{2}\left(cos\frac{A-B}{2}+sin\frac{C}{2}\right)-1\)
\(=2sin\frac{C}{2}\left(cos\frac{A-B}{2}+cos\frac{A+B}{2}\right)-1\)
\(=4cos\frac{A}{2}cos\frac{B}{2}sin\frac{C}{2}-1\)
15 tháng 4 2017
Ta có bất phương trình tương đương:
\(\Leftrightarrow x-2\left(\cos B+\cos C\right)x+2-2\cos A\ge0\)
Ta có:
\(\Delta'=\left(\cos B+\cos C\right)^2-2+2\cos A\)
\(=4\cos^2\left(\frac{B+C}{2}\right).\cos^2\left(\frac{B-C}{2}\right)-4\sin^2\left(\frac{A}{2}\right)\)
\(=4\sin^2\left(\frac{A}{2}\right)\left(\cos^2\left(\frac{B-C}{2}\right)-1\right)\le0\)
Bên cạnh đó ta có hệ số \(a=1>0\)
Từ đây ta suy ra điều phải chứng minh là đúng.
29 tháng 10 2021
Xét tam giác ABC nhọn có \(BC^2=AB^2+AC^2-2AB\cdot AC\cdot\cos\widehat{A}\)
\(\Rightarrow\cos\widehat{A}=\dfrac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4\cdot\dfrac{1}{2}AB\cdot AC}=\dfrac{AB^2+AC^2-BC^2}{4S_{ABC}}\)
Cmtt: \(\left\{{}\begin{matrix}\cos\widehat{B}=\dfrac{AB^2+BC^2-AC^2}{4S_{ABC}}\\\cos\widehat{C}=\dfrac{AC^2+BC^2-AB^2}{4S_{ABC}}\end{matrix}\right.\)
\(\Rightarrow\cos\widehat{A}+\cos\widehat{B}+\cos\widehat{C}\\
=\dfrac{AB^2+AC^2-BC^2+AB^2+BC^2-AC^2+AC^2+BC^2-AB^2}{4S_{ABC}}\\
=\dfrac{AB^2+AC^2+BC62}{4S_{ABC}}\)