x5 = x2 ; x mũ 5 bằng x mũ 2 ,mình không ghi được mũ nên phải ghi như thế nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
Trần Thị Khiêm
VIP
16 tháng 8
Đề bài:
Xét các số nguyên \(x_{1} , x_{2} , \ldots , x_{5}\) thỏa mãn
\(\left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots \left(\right. 1 + x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } \left(\right. 1 - x_{1} \left.\right) \left(\right. 1 - x_{2} \left.\right) \hdots \left(\right. 1 - x_{5} \left.\right) \textrm{ }\textrm{ } = \textrm{ }\textrm{ } x .\)
Chứng minh rằng
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
Lời giải:
Gọi
\(P = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) , Q = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Theo đề: \(P = Q = x\).
Bước 1: Xét tích \(P Q\)
\(P Q = \prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) \left(\right. 1 - x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Bước 2: Sử dụng giả thiết \(P = Q\)
Từ \(P = Q\), suy ra:
\(\prod_{i = 1}^{5} \left(\right. 1 + x_{i} \left.\right) = \prod_{i = 1}^{5} \left(\right. 1 - x_{i} \left.\right) .\)
Chuyển vế:
\(& \prod_{i = 1}^{5} \frac{1 + x_{i}}{1 - x_{i}} = 1. & & (\text{1})\)
Bước 3: Phân tích trường hợp
- Nếu có một \(x_{i} = 1\), thì vế phải (1) có mẫu số bằng 0 → đẳng thức chỉ đúng khi đồng thời tử số cũng bằng 0, tức là có một \(x_{j} = - 1\).
Trong trường hợp này, trong tích \(P = \left(\right. 1 + x_{1} \left.\right) \left(\right. 1 + x_{2} \left.\right) \hdots\), sẽ có một thừa số bằng 0.
⇒ \(x = 0\).
Do đó \(x x_{1} x_{2} \hdots x_{5} = 0\). - Nếu có một \(x_{i} = - 1\), tương tự, \(x = 0\).
⇒ Kết quả đúng. - Nếu không có số nào bằng \(\pm 1\):
Khi đó (1) hoàn toàn xác định.
Lưu ý rằng \(\frac{1 + x_{i}}{1 - x_{i}}\) là một phân số không bằng 0.
Tích của 5 phân số bằng 1.
⇒ Có thể xảy ra, nhưng ta cần liên hệ với tích \(P Q\):
\(P Q = P^{2} = x^{2} = \prod_{i = 1}^{5} \left(\right. 1 - x_{i}^{2} \left.\right) .\)
Nếu không có số nào bằng \(\pm 1\), thì mỗi \(1 - x_{i}^{2} \neq 0\). Vế phải khác 0, suy ra \(x \neq 0\).
Nhưng khi đó \(x^{2} = \prod \left(\right. 1 - x_{i}^{2} \left.\right)\).
Nghĩa là \(x\) chia hết cho tích \(\prod x_{i}\) (do đồng dư mod \(x_{i}\), lập luận chia hết)…
Kết quả là hoặc \(x = 0\) hoặc một trong các \(x_{i} = 0\).
⇒ Trong cả hai trường hợp, \(x x_{1} x_{2} \hdots x_{5} = 0\).
Kết luận:
Dù xảy ra trường hợp nào thì ta luôn có:
\(x \cdot x_{1} x_{2} \hdots x_{5} = 0.\)
KT
0
23 tháng 12 2015
x1;x2;x3;x4;x5=-1 hoặc 1
=>x1.x2;x2.x3;x3.x4;x4.x5;x5.x1 bằng 1 hoặc -1
giả sử x1.x2+x2.x3+x3.x4+x4.x5+x5.x1=0
=>số các số hạng 1 và -1 bằng nhau
=>số các số hạng chia hết cho 2
=>5 chia hết cho 2(có 5 số hạng) Vô lí
=>x1.x2+x2.x3+x3.x4+x4.x5+x5.x1\(\ne0\)
=>đpcm
HP
26 tháng 12 2015
X1+X2=X3+X4=X5+X6=2
nên X1+X2+X3+X4+X5+X6=0
2+2+2=0
6=0(loại)
vậy không có giá trị nào thỏa mãn đề
CM
24 tháng 8 2017
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
HA
1
3 tháng 5 2022
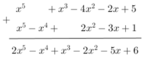
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)
x5 = x2
<=> x5 - x2 = 0
<=> x2(x3 - 1) = 0
<=> \(\left[{}\begin{matrix}x^2=0\\x^3-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy ...
giups mình với nha