Tìm số nguyên dương n để n100 + n50 + 1 là số nguyên tố
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 7 2017
Lấy căn bậc 50 mỗi vế của bất phương trình ta nhận được
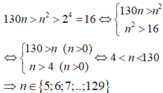
Từ đó có 125 số nguyên dương n thỏa mãn điều kiện đã cho
Chọn D
IL
1
KT
26 tháng 7 2018
\(P=n^3-n^2+n-1\)
\(=n^2\left(n-1\right)+\left(n-1\right)\)
\(=\left(n-1\right)\left(n^2+1\right)\)
Đế P là số nguyên tố thì: \(\orbr{\begin{cases}n-1=1\\n^2+1=1\end{cases}}\) \(\Leftrightarrow\)\(\orbr{\begin{cases}n=2\left(TM\right)\\n=0\left(L\right)\end{cases}}\)
Vậy n= 2
9 tháng 8 2019
Em tham khảo!
Câu 3: Câu hỏi của trần như - Toán lớp 8 - Học toán với OnlineMath
Câu 2: Câu hỏi của Hoàng Bình Minh - Toán lớp 8 - Học toán với OnlineMath
NQ
1
TN
1
VC
2
18 tháng 2 2017
để n là số nguyên tố suy ra n+8 chia hết cho 2n-5
suy ra:n+8 chia hết cho 2n-5 suy ra:2n+16 chia hết cho 2n-5
và 2n-5 chia hết cho 2n-5 và 2n-5 chia hết cho 2n-5
suy ra [2n+16-2n+5]chia hết cho 2n-5
21 chia hết cho 2n-5
sau đó bạn tìm n rồi thay vào n+8/2n-5 rồi chọn kết quả nguyên tố tương ứng với n
nhớ bấm đúng cho mình nha
SL
1
VV
31 tháng 12 2015
PTTNT: n^4 + 4 = ( n^2 + 2 )^2 - 4n^2
= ( n^2 + 2 ) - (2n)^2
= ( n^2 + 2 - 2n )( n^2 + 2 + 2n )
=> 1