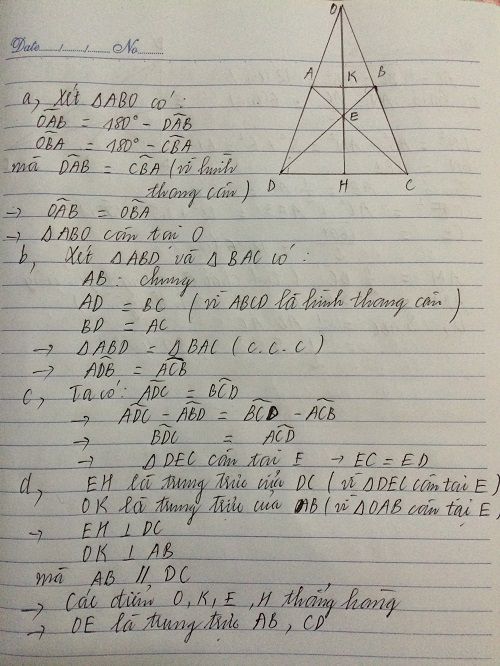cho tam giác ABC cân ở A có BD và CE là 2 đường trung tuyến.Chứng minh rằng :BCDE là hình thang cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 8 2017
Sử dụng tính chất đường trung bình, ta chứng minh được DE//BC
27 tháng 8 2021
Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: DE//CB
Xét tứ giác BEDC có DE//BC
nên BEDC là hình thang
mà \(\widehat{EBC}=\widehat{DCB}\)
nên BEDC là hình thang cân
27 tháng 8 2021
bạn ơi bạn chứng minh sai rùi ở cuối ý nếu mà 2 góc đáy bằng nhau chưa chắc đã là hình thang cân đâu chẳng hạn hình vuông 2 đáy cũng = nhau ......
nên bạn cm sai rùi sửa lại đi bạn cm 2 đường chéo bằng nhau
4 tháng 7 2021
a) Ta có: \(AD=DC=\dfrac{AC}{2}\)(D là trung điểm của AC)
\(AE=EB=\dfrac{AB}{2}\)(E là trung điểm của AB)
mà AC=AB(ΔBAC cân tại A)
nên AD=DC=AE=EB
Xét ΔADE có AE=AD(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔADB và ΔAEC có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
AD=AE(cmt)
Do đó: ΔADB=ΔAEC(c-g-c)
c) Ta có: ΔAED cân tại A(gt)
nên \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔAED cân tại A)(1)
Ta có: ΔABC cân tại A(gt)
nên \(\widehat{ABC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AED}=\widehat{ABC}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên ED//BC(Dấu hiệu nhận biết hai đường thẳng song song)
Xét tứ giác BCDE có ED//BC(cmt)
nên BCDE là hình thang có hai đáy là ED và BC(Định nghĩa hình thang)
Hình thang BCDE(ED//BC) có BD=EC(ΔADB=ΔAEC)
nên BCDE là hình thang cân(Dấu hiệu nhận biết hình thang cân)
27 tháng 8 2021
BD và CE là 2 đường trung tuyến.
=> EA=EB , DA=DC
ΔABC cân tại A=> AB=AC
=> AE=AD=> ΔAED cân tại A
. Xét ΔABD và Δ ACE có:
góc A chung
AB=AC (GT)
AD=AE (chứng minh trên)
=> ΔABD = ΔACE( c.g.c)
. EA = EB , DA=DC => ED là đườn TB của Δ ABC => ED //BC => tứ giác BCDE là hình thang
ΔABD = ΔACE => BD = CE ( Hai cạnh tương ứng)
=> BCDE là hình thang cân
19 tháng 7 2017
a) Ta có : \(\Delta\)ABC cân tại A =.>AB=AC mà BD là trung tuyến =.>AD=DC ;CE là trung tuyến => AE=EB
=> AE=AD
=>\(\Delta\)AED cân tại a
KV
30 tháng 8 2023
a) Do ∆ABC cân tại A
⇒ AB = AC (1)
Do BD là đường trung tuyến
⇒ D là trung điểm của AC
⇒ AD = CD (2)
Do CE là đường trung tuyến
⇒ E là trung điểm của AB
⇒ AE = BE (3)
Từ (1), (2) và (3)
⇒ AE = AD
∆AED có:
⇒ AE = AD (cmt)
⇒ ∆AED cân tại A
b) ∆AED cân tại A (cmt)
⇒ ∠AED = ∠ADE = (180⁰ - ∠A) : 2 (4)
∆ABC cân tại A
⇒ ∠ABC = ∠ACB = (180⁰ - ∠A) : 2 (5)
Từ (4) và (5)
⇒ ∠AED = ∠ABC
Mà ∠AED và ∠ABC là hai góc đồng vị
⇒ ED // BC
Tứ giác BCDE có:
ED // BC (cmt)
⇒ BCDE là hình thang
Mà ∠CBE = ∠BCD (∆ABC cân tại A)
⇒ BCDE là hình thang cân