Bài 1: Cho đường tròn tâm O, bán kính 10cm và dây AB = 12cm. Tính khoảng cách từ tâm O đến dây AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình sẽ không vẽ hình vì sợ duyệt.
Vì (O) có bán kính 10cm nên \(OA=10cm\)
Gọi OH là khoảng cách từ O đến AB, khi đó theo quan hệ vuông góc giữa đường kính và dây, ta có H là trung điểm AB, từ đó \(AB=2AH\)
Đồng thời, \(OH=8cm\)
\(\Delta OAH\)vuông tại H \(\Rightarrow AH=\sqrt{OA^2-OH^2}=\sqrt{10^2-8^2}=6\left(cm\right)\)
\(\Rightarrow AB=2AH=2.6=12\left(cm\right)\)
\(\Rightarrow\)Chọn A

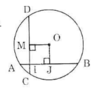
a) Kẻ OJ vuông góc với AB tại J.
Theo quan hệ vuông góc giữa đường kính và dây suy ra: J là trung điểm của AB.
![]()
Áp dụng định lí Pitago trong tam giác vuông OAJ có:
OJ2 = OA2 – AJ2 = 52 – 42 = 9 (OA = R = 5cm)
=> OJ = 3cm (1)
Vậy khoảng cách từ tâm O đến dây AB là OJ = 3cm.

 ∆OBH vuông tại H
∆OBH vuông tại H
⇒ OB² = OH² + BH² (Pytago)
⇒ BH² = OB² - OH²
= 5² - 4²
= 9
⇒ BH = 3 (cm)
Do OH ⊥ AB
⇒ H là trung điểm của AB
⇒ AB = 2BH = 2.3 = 6 (cm)
Gọi OH là khoảng cách từ tâm O đến dây AB
=>OH\(\perp\)AB tại H
=>OH=4cm
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(HA^2+4^2=5^2\)
=>\(HA^2=5^2-4^2=9\)
=>HA=3(cm)
H là trung điểm của AB
=>\(AB=2\cdot AH=6\left(cm\right)\)

Xét (O) có
OH là một phần đường kính
AB là dây
OH\(\perp\)AB tại H
Do đó: H là trung điểm của AB
=>AH=AB/2=6(cm)
Xét ΔOHA vuông tại H có
\(OA^2=OH^2+AH^2\)
hay OH=8cm

Câu 1:
Gọi giao điểm của OC với AB là H
Vì OC\(\perp\)AB nên OH\(\perp\)AB tại H
=>OH là khoảng cách từ O xuống dây AB
Ta có: ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
=>HA=HB=AB/2=8(cm)
ΔOHA vuông tại H
=>\(OH^2+HA^2=OA^2\)
=>\(OH^2=10^2-8^2=36\)
=>\(OH=\sqrt{36}=6\left(cm\right)\)
Câu 2:
a: Xét (O) có
AB là đường kính
BC là dây
Do đó: AB>BC
b: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
c: Xét ΔACB có
O là trung điểm của AB
OM//CB
Do đó: M là trung điểm của AC

Vì \(AB\perp MN\) tại H nên H là trung điểm AB (dây vuông góc đường kính)
\(\Rightarrow AH=\dfrac{1}{2}AB=6\left(cm\right)\)
MH vừa là đường cao vừa là trung tuyến nên \(\Delta MAB\) cân tại M
Do đó \(MA=MB=10\left(cm\right)\)
Ta có \(\widehat{MAN}=90^0\)(góc nt chắn nửa đường tròn) nên tam giác MAN vuông tại A
Áp dụng HTL tam giác
\(\dfrac{1}{AH^2}=\dfrac{1}{AN^2}+\dfrac{1}{AM^2}\\ \Rightarrow\dfrac{1}{36}=\dfrac{1}{AN^2}+\dfrac{1}{100}\\ \Rightarrow\dfrac{1}{AN^2}=\dfrac{1}{36}-\dfrac{1}{100}=\dfrac{4}{225}\\ \Rightarrow4AN^2=225\Rightarrow AN^2=\dfrac{225}{4}\Rightarrow AN=\dfrac{15}{2} =7,5\left(cm\right)\)
\(MN=\sqrt{AN^2+AM^2}=\sqrt{10^2+7,5^2}=12,5\left(cm\right)\)
Vậy đường kính đường tròn \(\left(O\right)\) dài 12,5 cm
NH vừa là đường cao vừa là trung tuyến nên \(\Delta NAB\) cân tại N
OK vuông góc với MB nên K cũng là trung điểm MB
\(\Rightarrow AN=NB=7,5\left(cm\right)\)
\(\left\{{}\begin{matrix}NO=OM\left(=R\right)\\MK=KB\left(cm.trên\right)\end{matrix}\right.\Rightarrow OK\) là đtb tam giác MBN
\(\Rightarrow OK=\dfrac{1}{2}NB=\dfrac{1}{2}\cdot7,5=3,75\left(cm\right)\)

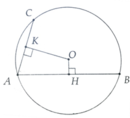
Gọi OH,OK Lần lượt là khoảng cách từ O đến AB,AC
Tính được OH = 41 2 cm và OH = 2 2 cm
Lời giải:
Gọi dây trên là dây AB. Hạ OH⊥⊥AB = {H} (cd)
Xét (O) 1 phần đường kính OH: OH⊥⊥AB = {H} (cd)
=> H là trung điểm AB (đl) => HA = HB = AB: 2 = 12:2 = 6 (cm)
OH⊥⊥AB = {H} (cd) => ΔΔOHB vuông tại H (đn)
=> OH22+ HB22= OB22(Đl Py-ta-go)
T/s: OH22+ 622= R22
<=> OH22+36 = 1022=100
<=> OH22= 64 => OH = 8 (cm)
Gọi H là chân đường cao kẻ từ O
=> H là trung điểm AB
=> AH = AB/2 = 12/2 = 6 cm
Theo định lí Pytago cho tam giác AOH vuông tại H
\(AO^2=OH^2+AH^2\Rightarrow OH^2=AO^2-AH^2=100-36=64\Rightarrow OH=8\)cm