Cho tứ giác ABCD biết AB=AD, BC=CD.Chứng minh AC⊥BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 11 2022
1/nối AC
Do AB//CD=>BAC=ACD(so le trong)
Do AD//BC=>ACB=DAC(so le trong)
Xét ∆ABC và ∆ACD
ACB=DAC(chứng minh trên)
BAC=DAC(chứng minh trên)
AC chung
Vậy ∆ABC=∆CDA(g.c.g)=>AB=DC(cặp cạnh tương ứng)
AD=BC(cặp cạnh tương ứng)
N
1
2 tháng 7
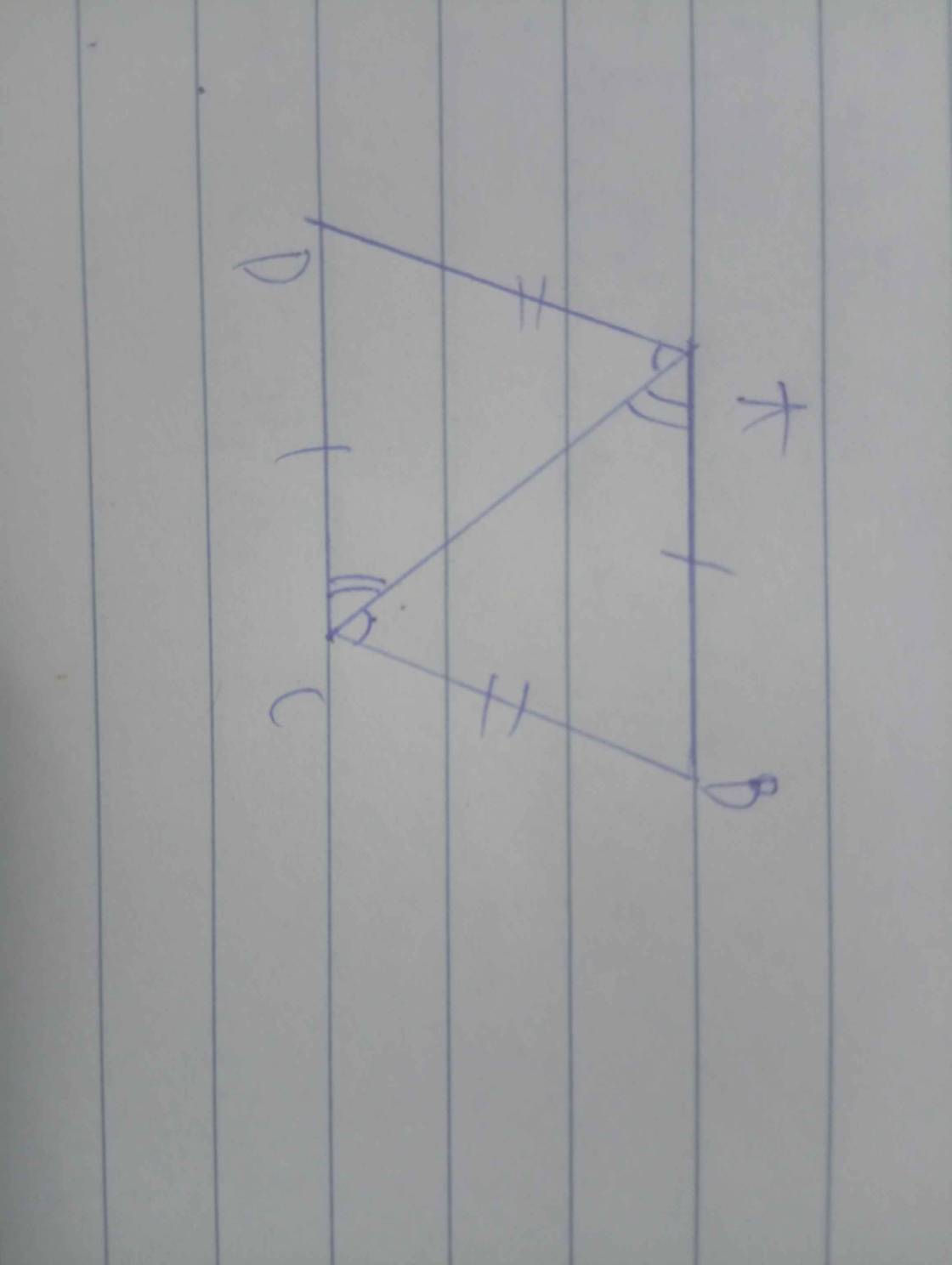
Giải:
Gọi \(O\) là giao điểm của hai đường chéo \(A C\) và \(B D\).
Xét tam giác \(A B O\), ta có:
\(O A + O B > A B\) (bất đẳng thức tam giác)
Xét tam giác \(D C O\), ta có:
\(O C + O D > C D\) (bất đẳng thức tam giác)
Cộng hai bất đẳng thức trên:
\(A C + B D > A B + C D\)
Mà theo giả thiết:
\(A B + B D \leq A C + C D\)
Cộng hai vế bất đẳng thức ta được:
\(2 A C + B D + C D > 2 A B + B D + C D\)
Rút gọn vế trái và vế phải:
\(2 A C > 2 A B\)
Suy ra: \(A C > A B\), hay \(A B < A C\) \(\left(đpcm\right)\).
KC
0
AB=AD, BC=CD
=>Tứ giác ABCD là hình chữ nhật
=>AC⊥BD