cho các số x, y, z thỏa mãn x+y+z=\(\dfrac{3}{2}\) . chứng minh rằng x^2+y^2+z^2≥\(\dfrac{3}{4}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Đề bài chắc chắn là có vấn đề
Thử với \(x=y=z=\dfrac{1}{3}\) thì \(VT=\dfrac{\sqrt{2}}{4}< 2\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
Như bạn sửa điều kiện thành \(x^3+y^3+z^3=1\) thì dấu "=" không xảy ra
Việc chứng minh vế trái lớn hơn 2 (một cách tuyệt đối) khá đơn giản:
\(\dfrac{x^2}{\sqrt{1-x^2}}=\dfrac{x^3}{x\sqrt{1-x^2}}\ge\dfrac{x^3}{\dfrac{x^2+1-x^2}{2}}=2x^3\)
Làm tương tự với 2 số hạng còn lại, sau đó cộng vế
Nhưng đẳng thức không xảy ra.
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 4 2021
\(VT\le\dfrac{x}{2x+2y+2}+\dfrac{y}{2yz+2z+2}+\dfrac{z}{2z+2x+2}\)
Nên ta chỉ cần chứng minh: \(\dfrac{x}{x+y+1}+\dfrac{y}{y+z+1}+\dfrac{z}{z+x+1}\le1\)
\(\Leftrightarrow\dfrac{y+1}{x+y+1}+\dfrac{z+1}{y+z+1}+\dfrac{x+1}{z+x+1}\ge2\)
Thật vậy, ta có:
\(VT=\dfrac{\left(x+1\right)^2}{\left(x+1\right)\left(z+x+1\right)}+\dfrac{\left(y+1\right)^2}{\left(y+1\right)\left(x+y+1\right)}+\dfrac{\left(z+1\right)^2}{\left(z+1\right)\left(y+z+1\right)}\)
\(VT\ge\dfrac{\left(x+y+z+3\right)^2}{\left(x^2+y^2+z^2\right)+3\left(x+y+z\right)+xy+yz+zx+3}\)
\(VT\ge\dfrac{6\left(x+y+z\right)+2\left(xy+yz+zx\right)+12}{3\left(x+y+z\right)+xy+yz+zx+6}=2\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\)
1 tháng 2 2023
Áp dụng BĐT cô si với ba số không âm ta có :
1(x+1)2+x+18+x+18≥33√164=341(�+1)2+�+18+�+18≥31643=34
=> 1(x+1)2≥34−x+141(�+1)2≥34−�+14 (1)
Dấu '' = '' xảy ra khi x = 1
CM tương tự ra có " 1(y+1)2≥34−y+141(�+1)2≥34−�+14(2) ; 1(z+1)2≥34−z+141(�+1)2≥34−�+14 (3)
Dấu ''= '' xảy ra khi y = 1 ; z = 1
Từ (1) (2) và (3) => 1(x+1)2+1(y+1)2+1(z+1)2≥34⋅3−x+y+z+341(�+1)2+1(�+1)2+1(�+1)2≥34⋅3−�+�+�+34≥94−33√xyz+34=94−64=34≥94−3���3+34=94−64=34
BĐT được chứng minh
Dấu '' = '' của bất đẳng thức xảy ra khi x =y =z = 1
:()
8 tháng 12 2023
Có \(VT=\dfrac{x^2}{x^3-xyz+2013x}+\dfrac{y^2}{y^3-xyz+2013y}+\dfrac{z^2}{z^3-xyz+2013z}\)
\(\ge\dfrac{\left(x+y+z\right)^2}{x^3+y^3+z^3-3xyz+2013\left(x+y+z\right)}\)
\(=\dfrac{\left(x+y+z\right)^2}{\left(x+y+z\right)\left[x^2+y^2+z^2-\left(xy+yz+zx\right)\right]+2013\left(x+y+z\right)}\)
\(=\dfrac{x+y+z}{x^2+y^2+z^2-\left(xy+yz+zx\right)+3\left(xy+yz+zx\right)}\)
(vì \(2013=3.671=3\left(xy+yz+zx\right)\))
\(=\dfrac{x+y+z}{x^2+y^2+z^2+2\left(xy+yz+zx\right)}\)
\(=\dfrac{x+y+z}{\left(x+y+z\right)^2}\)
\(=\dfrac{1}{x+y+z}\)
ĐTXR \(\Leftrightarrow\dfrac{1}{x^2-yz+2013}=\dfrac{1}{y^2-zx+2013}=\dfrac{1}{z^2-xy+2013}\)
\(\Leftrightarrow x^2-yz=y^2-zx=z^2-xy\)
\(\Leftrightarrow x=y=z\) (với \(x,y,z>0\))
Vậy ta có đpcm.
17 tháng 7 2021
đặt\(A=\dfrac{x^3}{2x+3y+5z}+\dfrac{y^3}{2y+3z+5x}+\dfrac{z^3}{2z+3x+5y}\)
\(=>A=\dfrac{x^4}{2x^2+3xy+5xz}+\dfrac{y^4}{2y^2+3yz+5xy}+\dfrac{z^4}{2z^2+3xz+5yz}\)
BBDT AM-GM
\(=>A\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{2\left(x^2+y^2+z^2\right)+8\left(xy+yz+xz\right)}\)
theo BDT AM -GM ta chứng minh được \(xy+yz+xz\le x^2+y^2+z^2\)
vì \(x^2+y^2\ge2xy\)
\(y^2+z^2\ge2yz\)
\(x^2+z^2\ge2xz\)
\(=>2\left(x^2+y^2+z^2\right)\ge2\left(xy+yz+xz\right)< =>xy+yz+xz\le x^2+y^2+z^2\)
\(=>2\left(x^2+y^2+z^2\right)+8\left(xy+yz+xz\right)\le10\left(x^2+y^2+z^2\right)\)
\(=>A\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{10\left(x^2+y^2+z^2\right)}=\dfrac{x^2+y^2+z^2}{10}=\dfrac{\dfrac{1}{3}}{10}=\dfrac{1}{30}\left(đpcm\right)\)
dấu"=" xảy ra<=>x=y=z=1/3
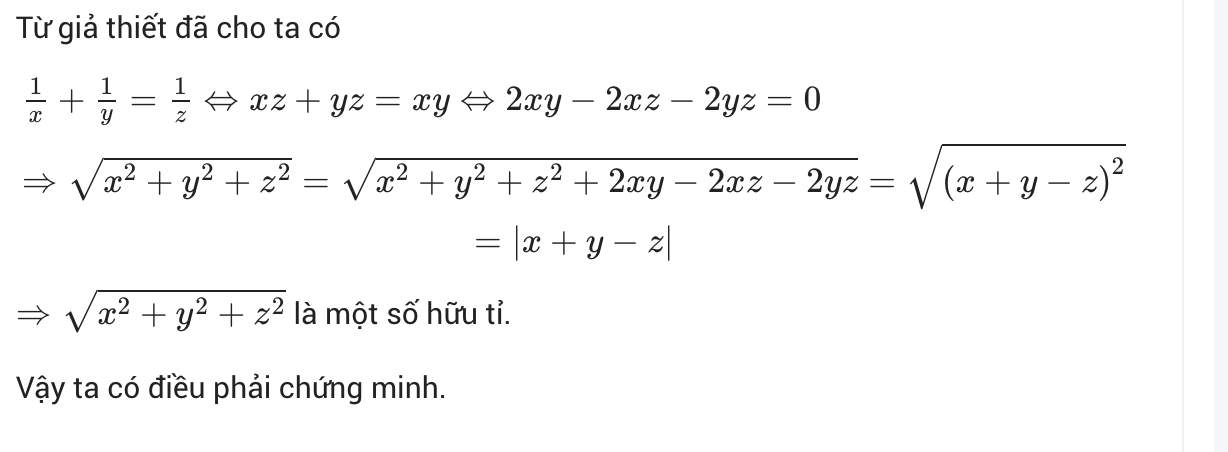
Áp dụng BĐT Bunhyaxcopki, ta có:
\(\left(x^2+y^2+z^2\right)\left(1^2+1^2+1^2\right)\ge\left(x+y+z\right)^2\)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\left(\dfrac{3}{2}\right)^2\)
\(\Leftrightarrow3\left(x^2+y^2+z^2\right)\ge\dfrac{9}{4}\)
\(\Leftrightarrow x^2+y^2+z^2\ge\dfrac{3}{4}\)
ủng hộ cách khác không xài bđt bunhia:
\(x^2+y^2+z^2\ge\dfrac{3}{4}\)
\(\Leftrightarrow x^2+y^2+z^2-x-y-z\ge\dfrac{3}{4}-\dfrac{3}{2}=-\dfrac{3}{4}\)
\(\Leftrightarrow x^2+y^2+z^2-x-y-z+\dfrac{3}{4}\ge0\)
\(\Leftrightarrow\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2-y+\dfrac{1}{4}\right)+\left(z^2-z+\dfrac{1}{4}\right)\ge0\)
\(\Leftrightarrow\left(x-\dfrac{1}{2}\right)^2+\left(y-\dfrac{1}{2}\right)^2+\left(z-\dfrac{1}{2}\right)^2\ge0\)(luôn đúng \(\forall x+y+z=\dfrac{3}{2}\))