Cho tứ giác ABCD nội tiếp đg rèn tâm O bk R. Cmr nếu AB2+CD2 =4R2 thì AC vg góc vs BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 6 2017
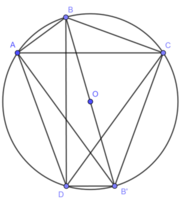
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: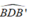
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do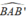 
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)
TK
0
13 tháng 1 2021
Bài này là định lý khá cơ bản của tứ giác điều hoà.
Do AM, AC đẳng giác của góc BAD nên dễ dàng chứng minh được:
\(\widehat{BAM}=\widehat{CAD}\).
Mặt khác do tứ giác ABCD nội tiếp nên \(\widehat{ABM}=\widehat{ACD}\).
Từ đó \(\Delta ABM\sim\Delta ACD(g.g)\)
\(\Rightarrow\dfrac{AB}{BM}=\dfrac{AC}{CD}\Rightarrow AB.CD=BM.AC\).
Chứng minh tương tự, ta cũng có \(AD.BC=CM.AC\).
Mà BM = CM nên \(AB.CD=AD.BC\) hay tứ giác ABCD điều hoà.
(Định lý đảo vẫn đúng).
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
16 tháng 7 2023
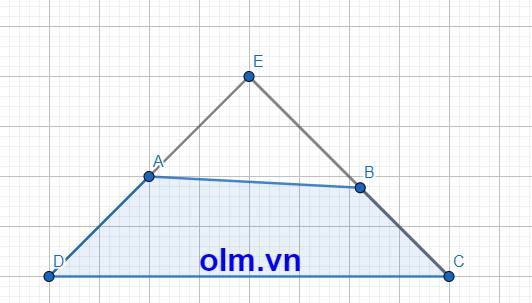
Kéo dài DA và CB lần lượt về phía A và B cắt nhau tại E
Xét tam giác DCE có \(\widehat{DEC}\) = 1800 - (\(\widehat{EDC}\) + \(\widehat{ECD}\)) = 1800- 900 = 900
⇒\(\Delta\)DEC vuông tại E
Xét \(\Delta\)AEB Theo pytago ta có: AE2 + BE2 = AB2
Tương tự ta có: DE2 + CE2 = DC2
Cộng vế với vế ta có: AE2 + BE2 + DE2 + CE2 = AB2+DC2
AE2 + CE2+BE2+DE2 = AB2+DC2 (1)
Xét \(\Delta\)AEC theo pytago ta có: AE2+ CE2 = AC2
Tương tự ta có: BE2 + DE2 = BD2
Cộng vế với vế ta có: AE2 + CE2 + BE2+ DE2 = AC2 + BD2 (2)
Từ (1) và (2) ta có: AC2 + BD2 = AB2 + DC2(đpcm)