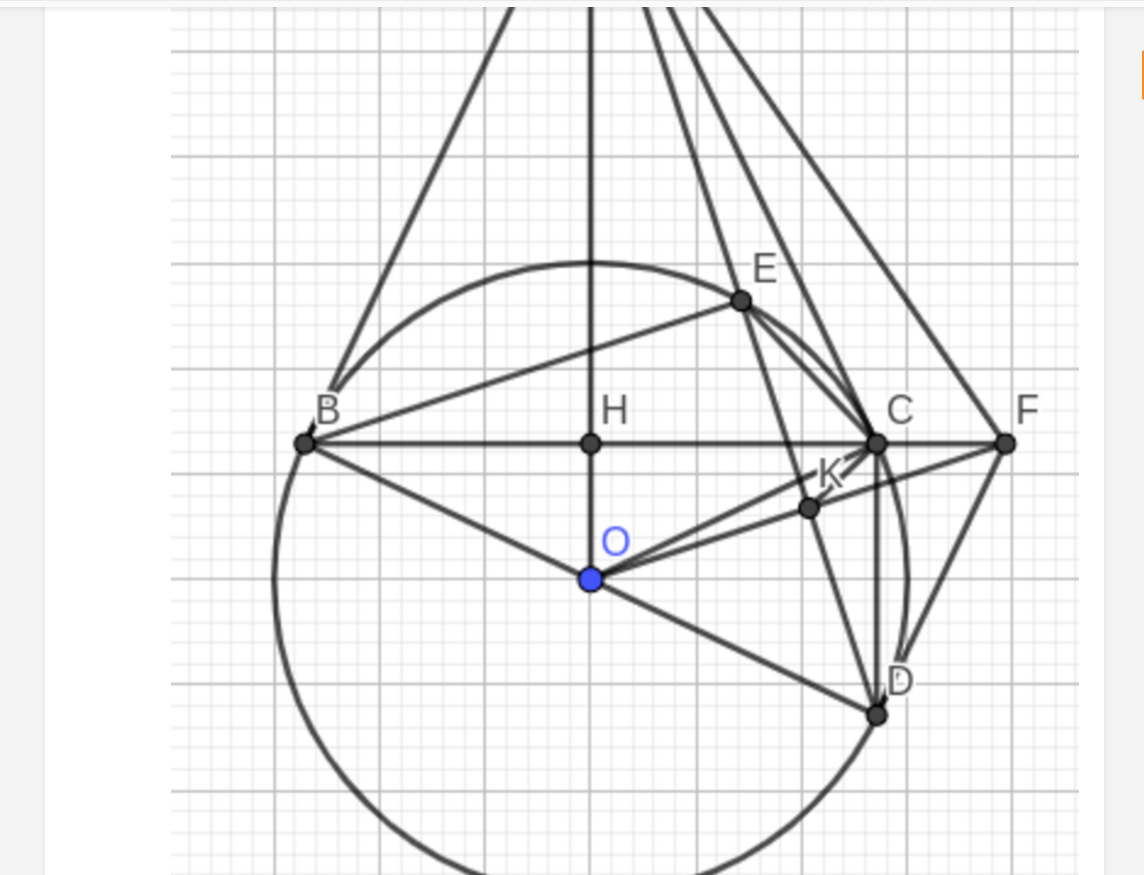
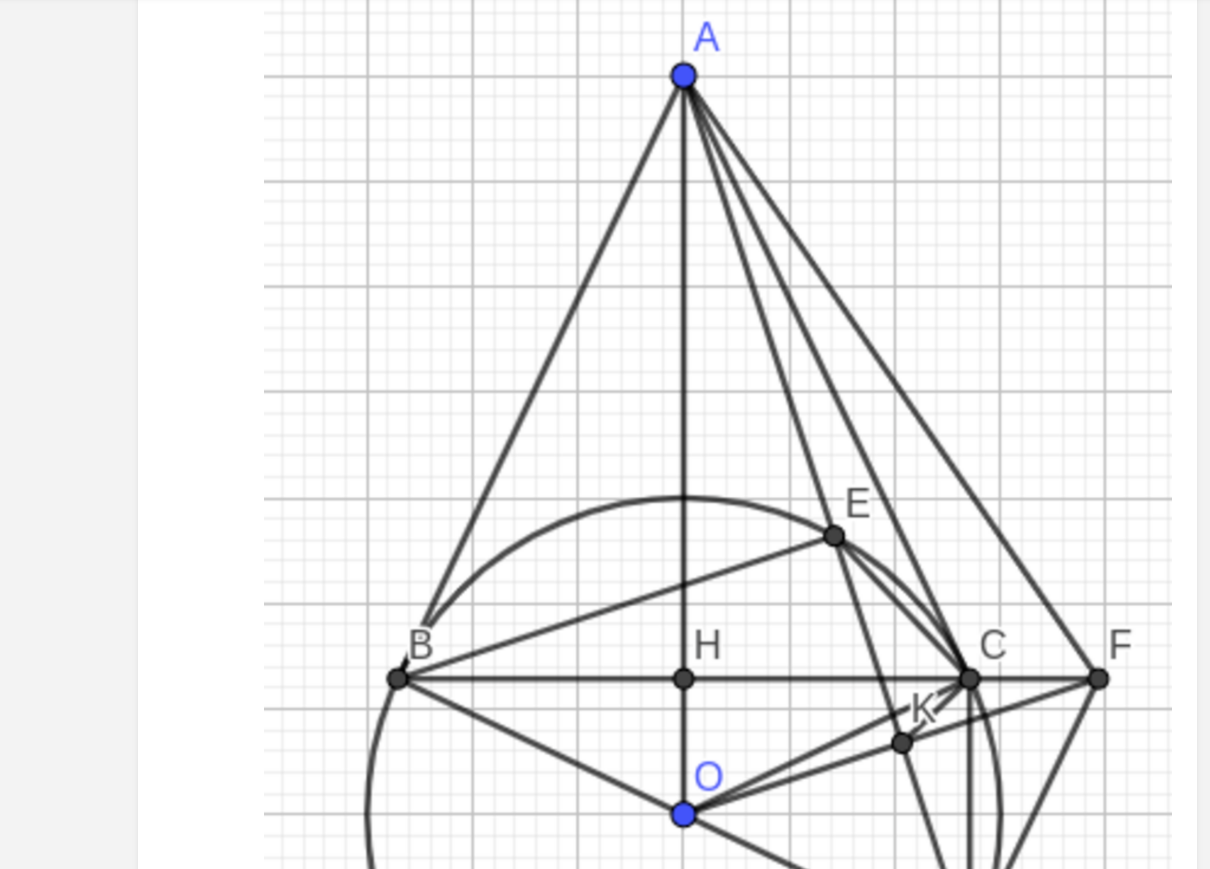
Bài 1: Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại B. Vẽ tiếp tuyến chung ngoài AC với A thuộc (O), C thuộc (O'). Tiếp tuyến chung trong tại B cắt AC tại M, MO cắt AB ở K, MO' cắt BC ở H.
a) Chứng minh tam giác ABC vuông.
b) Tính số do góc OMO'
c) Tính độ dài AC biết OB= 5cm, O'B = 3,2cm.
d) Tứ giác BKMH là hình gì? Vì sao?
e) Chứng minh dẳng thức MK.MO = MH.MO'
f) Chứng minh OO' là tiếp tuyến của đường tròn có đường kính AC.
g) Chứng minh AC là tiếp tuyến của đường tròn có đường kính OO'.
Bài 2: Cho đoạnthẳng AB, điểm C nằm giữa A và B. Vẽ về một phía của AB hai nửa đường tròn tâm O và P có đường kính theo thứ tự là AB và AC. Đường vuông góc với AB tại C cắt nửa đường tròn (P) tại M. Gọi N là chân đường vuôn góc kẻ từ C đến DB. Gọi Q là tâm nửa đường tròn ngoại tiếp tam giác CNB.
a) Xác định vị trí tương đối giữa các đường tròn (O) và (P) ; (O) và(Q) ; (P) và (Q).
b) Tứ giác DMCN là hình gì? Vì sao?
c) Chứng minh hệ thức DM.DA = DN.DB
d) Chứng minh MN là tiếp tuyến chung của các nửa đường tròn (P) và (Q)
e) Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC

giải b2:
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\) => PQ là tiếp tuyến của \(\left(O_2\right)\)
Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)

1: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
2: góc ACD=1/2*sđ cung AD=90 độ
ΔMAD vuông tại A có AC là đường cao
nên MA^2=MC*MD
Xét (O) có
MA,MB là tiếp tuyến
=>MA=MB
mà OA=OB
nên OM là trung trực của AB
=>OM vuông góc AB tại H
=>MH*MO=MA^2=MC*MD

Bài 1:
a: Xét tứ giác OAMB có \(\hat{OAM}+\hat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>O,A,M,B cùng thuộc một đường tròn
b: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
OA=OB
Do đó: ΔOAM=ΔOBM
=>MA=MB
c: OA=OB
=>O nằm trên đường trung trực của AB(1)
ta có: MA=MB
=>M nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
d: OM là đường trung trực của AB
=>OM⊥AB tại H và H là trung điểm của AB
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\) không đổi
Bài 2:
a; Xét (O) có
ΔAEB nội tiếp
AB là đường kính
Do đó:ΔAEB vuông tại E
=>BE⊥MA tại E
Xét (O) có
ΔAFB nội tiếp
AB là đường kính
Do đó: ΔAFB vuông tại F
=>AF⊥MB tại F
b: Xét tứ giác MEHF có \(\hat{MEH}+\hat{MFH}=90^0+90^0=180^0\)
nên MEHF là tứ giác nội tiếp đường tròn đường kính MH
=>M,E,H,F cùng thuộc một đường tròn
c: Vì MEHF nội tiếp đường tròn đường kính MH
mà I là trung điểm của MH
nên IM=IE=IF=IH
Gọi K là giao điểm của MH và AB
Xét ΔMAB có
AF,BE là các đường cao
AF cắt BE tại H
Do đó: H là trực tâm của ΔAMB
=>MH⊥AB tại K
IE=IH
=>ΔIEH cân tại I
=>\(\hat{IEH}=\hat{IHE}\)
=>\(\hat{IEH}=\hat{KHB}\)
\(\hat{IEO}=\hat{IEH}+\hat{OEH}\)
\(=\hat{KHB}+\hat{OBH}=\hat{KHB}+\hat{KBH}=90^0\)
=>IE⊥OE
d: Xét ΔIEO và ΔIFO có
IE=IF
OE=OF
IO chung
Do đó: ΔIEO=ΔIFO
=>\(\hat{IEO}=\hat{IFO}=90^0\)
=>I,E,O,F cùng thuộc một đường tròn