Cho tam giác ABC tìm tập hợp điểm M sao cho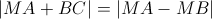 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
1
Những câu hỏi liên quan
CM
12 tháng 8 2019
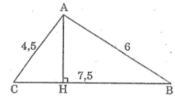
Tam giác ABC và tam giác MBC có chung cạnh đáy BC, đồng thời S A B C = S B M C nên khoảng cách từ M đến BC bằng khoảng cách từ A đến BC. Vậy M thay đổi cách BC một khoảng bằng AH nên M nằm trên hai đường thẳng x và y song song với BC cách BC một khoảng bằng AH.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
CM
12 tháng 10 2019
* Chứng minh thuận
Vì ΔCAB cân tại C nên CA = CB
Suy ra C thuộc đường trung trực của AB
Vì điểm C thay đổi mà ΔCAB luôn cân tại C nên C nằm trên đường trung trực của đường thẳng AB.
* Chứng minh đảo
Trên đường thẳng d lấy điểm C bất ký (C khác trung điểm M của AB).
Nối CA, CB.
Ta có: CA = CB (tính chất đường trung trực)
Suy ra tam giác CAB cân tại C.
Tập hợp các điểm C có tính chất CA = CB và ba điểm A, B, C không thẳng hàng là đường trung trực của AB ( trừ trung điểm M của AB).
18 tháng 5 2022
Khi ΔABC cân có đáy là AB thì ΔABC cân tại C
=>CA=CB
hay C nằm trên đường trung trực của AB
CM
13 tháng 11 2018
Gọi E và F lần lượt là trung điểm của AB; BC. Khi đó, ta có
M A → + M B → = M C → + M B → ⇔ 2 M E → = 2 M F → ⇔ M E → = M F →
Do đó, M thuộc đường trung trực của EF.
Đáp án C
Lời giải:
Lấy điểm $K$ sao cho $AKCB$ là hình bình hành
Khi đó: \(\overrightarrow{AK}=\overrightarrow {BC}\Leftrightarrow \overrightarrow{KA}+\overrightarrow{BC}=\overrightarrow{0}\)
Ta có:
\(|\overrightarrow{MA}+\overrightarrow{BC}|=|\overrightarrow{MA}-\overrightarrow{MB}|\)
\(\Leftrightarrow |\overrightarrow{MK}+\overrightarrow{KA}+\overrightarrow{BC}|=|\overrightarrow {BA}|\)
\(\Leftrightarrow |\overrightarrow{MK}|=|\overrightarrow{BA}|\)
Vậy tập hợp điểm M nằm trên đường tròn tâm $M$ bán kính \(R=AB\)