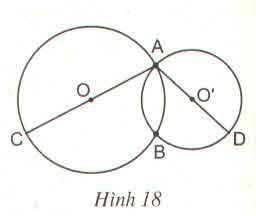
Chứng minh rằng 3 điểm C, B, D trên hình 18 thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi OO là giao ÁC,MDÁC,MD
ˆCHA=90∘⇒HO=AC2=MD2⇒ˆDHM=90∘CHA^=90∘⇒HO=AC2=MD2⇒DHM^=90∘
Tương tự ˆFHM=90∘⇒ˆDHF=90circ⇒D,H,FFHM^=90∘⇒DHF^=90circ⇒D,H,F thẳng hàng
Gọi II là giao DF,ACDF,AC
Đỏ ỐIỐI song song MF⇒IMF⇒I là trung điểm của DFDF
Kẻ II′⊥AB⇒I′II′⊥AB⇒I′ là trung điểm ABAB
Chứng minh II′=AB2⇒III′=AB2⇒I nằm trên đường trung trực của ABAB và cách ABAB một khoảng bằng AB2AB2

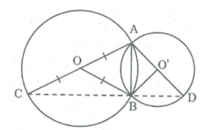
Nối AB, BO, BC, BO', BD.
* Trong ∆ ABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ∆ ABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ ∠ (ABC) = 90 0
* Trong ∆ ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))
Nên BO' là đường trung tuyến của tam giác ABD.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABD vuông tại B ⇒ ∠ (ABD) = 90 0
Ta có: ∠ (ABC) + ∠ (ABD) = ∠ (CBD) = 90 0 + 90 0 = 180 0
Vậy C, B, D thẳng hàng.