Trong mặt phẳng Oxy, cho đường tròn tâm \(I\left(3;-2\right)\), bán kính 3
a) Viết phương trình của đường tròn đó
b) Viết phương trình ảnh của đường tròn \(\left(I;3\right)\) qua phép tịnh tiến theo vectơ \(\overrightarrow{v}=\left(-2;1\right)\)
c) Viết phương trình ảnh của đường tròn \(\left(I;3\right)\) qua phép đối xứng qua trục Ox
d) Viết phương trình ảnh của đường tròn \(\left(I;3\right)\) qua phép đối xứng qua gốc tọa độ






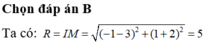
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là (%5E%7B2%7D) +
+ %5E%7B2%7D) = 9
= 9
b)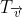 (I) = I' (1;-1), phương trình đường tròn ảnh :
(I) = I' (1;-1), phương trình đường tròn ảnh : 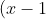%5E%7B2%7D&space;+&space;(y+1)%5E%7B2%7D&space;=&space;9)
c)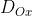 (I) = I'(3;2), phương trình đường tròn ảnh:
(I) = I'(3;2), phương trình đường tròn ảnh: %5E%7B2%7D&space;+&space;(y-2)%5E%7B2%7D&space;=&space;9)
d)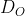 (I) = I'( -3;2), phương trình đường tròn ảnh:
(I) = I'( -3;2), phương trình đường tròn ảnh: %5E%7B2%7D&space;+&space;(y-2)%5E%7B2%7D&space;=&space;9)
Gọi I' là ảnh của I qua phép biến hình nói trên
a) Phương trình của đường tròn (I;3) là (%5E%7B2%7D) +
+ %5E%7B2%7D) = 9
= 9
b)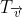 (I) = I' (1;-1), phương trình đường tròn ảnh :
(I) = I' (1;-1), phương trình đường tròn ảnh : 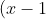%5E%7B2%7D&space;+&space;(y+1)%5E%7B2%7D&space;=&space;9)
c)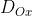 (I) = I'(3;2), phương trình đường tròn ảnh:
(I) = I'(3;2), phương trình đường tròn ảnh: %5E%7B2%7D&space;+&space;(y-2)%5E%7B2%7D&space;=&space;9)
d)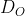 (I) = I'( -3;2), phương trình đường tròn ảnh:
(I) = I'( -3;2), phương trình đường tròn ảnh: %5E%7B2%7D&space;+&space;(y-2)%5E%7B2%7D&space;=&space;9)