Phát biểu định lý về dấu của một tam thức bậc hai \(f\left(x\right)=ax^2+bx+c\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
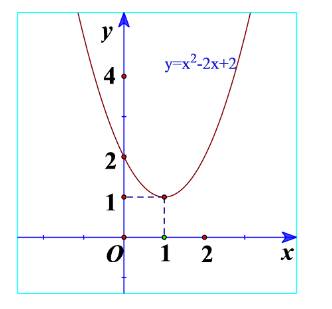
a) Ta thấy đồ thị nằm trên trục hoành nên \(f\left( x \right) = {x^2} - 2x + 2 > 0\).
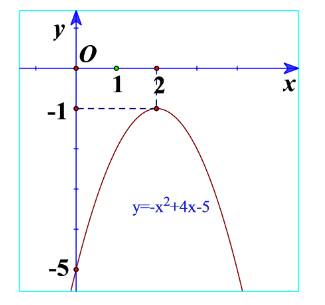
b) Ta thấy đồ thị nằm dưới trục hoành nên \(f\left( x \right) = - {x^2} + 4x - 5 < 0\).
c) Ta thấy \(f\left( x \right) = {x^2} - 2x + 2\) có hệ số a=1>0 và \(f\left( x \right) = {x^2} - 2x + 2 > 0\)
\(f\left( x \right) = - {x^2} + 4x - 5\) có hệ số a=-1
Như thế, khi \(\Delta < 0\) thì tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)\) cùng dấu với hệ số a.
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
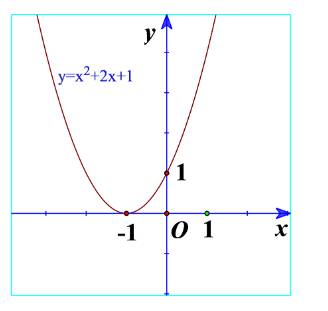
a) Từ đồ thị ta thấy \({x^2} + 2x + 1 \ge 0\forall x\)
Và \({x^2} + 2x + 1 > 0\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\)
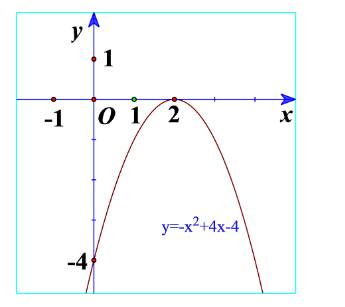
b) Từ đồ thị ta thấy \( - {x^2} + 4x - 4 \le 0\forall x\)
Và \( - {x^2} + 4x - 4 < 0\forall x \in \mathbb{R}\backslash \left\{ { - 2} \right\}\)
c) Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với dấu của hệ số a, với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
6 tháng 3 2018
Bài 1 : k bt làm
Bài 2 :
Ta có : \(\left(x-6\right).P\left(x\right)=\left(x+1\right).P\left(x-4\right)\) với mọi x
+) Với \(x=6\Leftrightarrow\left(6-6\right).P\left(6\right)=\left(6+1\right).P\left(6-4\right)\)
\(\Leftrightarrow0.P\left(6\right)=7.P\left(2\right)\)
\(\Leftrightarrow0=7.P\left(2\right)\)
\(\Leftrightarrow P\left(2\right)=0\)
\(\Leftrightarrow x=2\) là 1 nghiệm của \(P\left(x\right)\left(1\right)\)
+) Với \(x=-1\Leftrightarrow\left(-1-6\right).P\left(-1\right)=\left(-1+1\right).P\left(-1-4\right)\)
\(\Leftrightarrow\left(-7\right).P\left(-1\right)=0.P\left(-5\right)\)
\(\Leftrightarrow\left(-7\right).P\left(-1\right)=0\)
\(\Leftrightarrow P\left(-1\right)=0\)
\(\Leftrightarrow x=-1\) là 1 nghiệm của \(P\left(x\right)\) \(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Leftrightarrow P\left(x\right)\) có ót nhất 2 nghiệm
6 tháng 3 2018
nghiệm của đa thức xác định đa thức đó bằng 0
0 mà k bằng 0. You định làm nên cái nghịch lý ak -.-
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 2 2021
Với \(c=0\Rightarrow f\left(x\right)=0\) có nghiệm \(x=0\) (loại)
TH1: \(a;c\) trái dấu
Xét pt \(f\left(x\right)=0\Leftrightarrow a\left(ax^2+bx+c\right)^2+b\left(ax^2+bx+c\right)+c=0\)
Đặt \(ax^2+bx+c=t\) \(\Rightarrow at^2+bt+c=0\) (1)
Do a; c trái dấu \(\Leftrightarrow\) (1) luôn có 2 nghiệm trái dấu.
Không mất tính tổng quát, giả sử \(t_1< 0< t_2\)
\(\Rightarrow\left[{}\begin{matrix}ax^2+bx+c=t_1\\ax^2+bx+c=t_2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}ax^2+bx+c-t_1=0\left(2\right)\\ax^2+bx+c-t_2=0\left(3\right)\end{matrix}\right.\)
Mà a; c trái dấu nên:
- Nếu \(a>0\Rightarrow c< 0\Rightarrow c-t_2< 0\Rightarrow a\left(c-t_2\right)< 0\)
\(\Rightarrow\) (3) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)
- Nếu \(a< 0\Rightarrow c>0\Rightarrow c-t_1>0\Rightarrow a\left(c-t_1\right)< 0\)
\(\Rightarrow\left(2\right)\) có nghiệm hay \(f\left(x\right)=0\) có nghiệm (loại)
Vậy đa thức \(f\left(x\right)\) luôn có nghiệm khi a; c trái dấu
\(\Rightarrow\)Để \(f\left(x\right)=0\) vô nghiệm thì điều kiện cần là \(a;c\) cùng dấu \(\Leftrightarrow ac>0\)
Khi đó xét \(g\left(x\right)=0\) có \(a.\left(-c\right)< 0\Rightarrow g\left(x\right)=0\) luôn có 2 nghiệm trái dấu (đpcm)
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2024
\(\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta\le0\end{matrix}\right.\)
Quy tắc: tam thức bậc 2 ko đổi dấu khi \(\Delta< 0\) (có dấu = hay ko phụ thuộc đề yêu cầu \(f\left(x\right)\) có dấu = hay ko)
Khi đã có \(\Delta< 0\) thì dấu \(f\left(x\right)\) chỉ còn phụ thuộc a. Nếu a dương thì \(f\left(x\right)\) dương trên R, nếu a âm thì \(f\left(x\right)\) âm trên R.
Cách nhận biết đa thức
\(f\left(x\right)=ax^2+bx+c\)
Có nghiệm hay vô nghiệm
Lập \(\Delta\) ( đọc là delta )
\(\Delta=b^2-4ac\)
Nếu \(\Delta< 0\) : đa thức vô nghiệm
Nếu \(\Delta\ge0\) : đa thức có nghiệm
Nếu \(\Delta>0\) : đa thức có hai nghiệm
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)