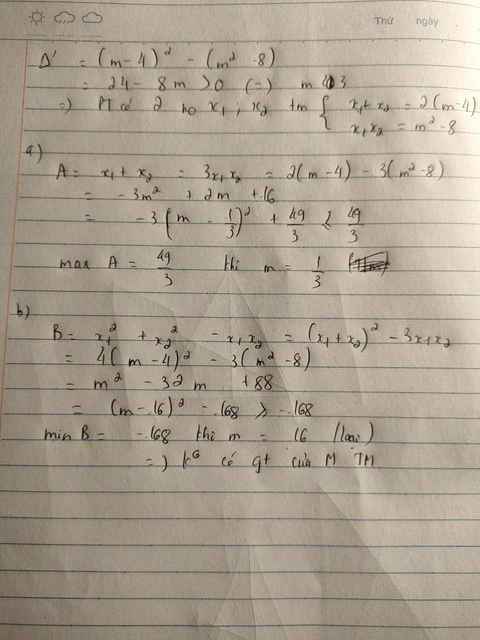Tìm các giá trị x thỏa mãn: |x-8|2010 = |x-8|4020
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
1
22 tháng 9 2015
I x-8 I10=Ix-8I20
=>Ix-8I10-Ix-8I20=0
=>Ix-8I10(1-Ix-8I10)=0
=>Ix-8I10=0 hoac 1-Ix-8I10=0
=>x=8 hoac x=9
LH
1
TN
Trần Ngọc Tuấn
VIP
18 tháng 2 2023
Đáp án: x=10,y=0x=10,y=0
Giải thích các bước giải:
Ta có:
x8−22y+3=712x8−22y+3=712
→x(2y+3)⋅12−2⋅8⋅12=7⋅8⋅(2y+3)→x(2y+3)⋅12−2⋅8⋅12=7⋅8⋅(2y+3)
→12x(2y+3)−192=56(2y+3)→12x(2y+3)−192=56(2y+3)
→12x(2y+3)−56(2y+3)=192→12x(2y+3)−56(2y+3)=192
→(12x−56)(2y+3)=192→(12x−56)(2y+3)=192
→(3x−14)(2y+3)=48→(3x−14)(2y+3)=48
Vì x,y∈Zx,y∈Z
→(3x−14,2y+3)→(3x−14,2y+3) là cặp ước của 4848
Mà 3x−143x−14 chia 33 dư 1,2y+31,2y+3 lẻ
→(3x−14,2y+3)∈{(16,3)}→(3x−14,2y+3)∈{(16,3)}
→(3x,2y)=(30,0)→(3x,2y)=(30,0)
→(x,y)=(10,0)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
\(y\ge\dfrac{8-x}{x+1}\Rightarrow P\ge4x+\dfrac{8-x}{x+1}+3=\dfrac{4x^2+6x+11}{x+1}=\dfrac{4x^2-4x+1+10\left(x+1\right)}{x+1}=\dfrac{\left(2x-1\right)^2}{x+1}+10\ge10\)
\(P_{min}=10\) khi \(\left(x;y\right)=\left(\dfrac{1}{2};5\right)\)
25 tháng 2 2022
\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16