Cho tam giác MNP vuông tại M có đường cao MK.
Tính cos ∠MP N, tan ∠MNP biết MK = 2√3 và PK = 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 5 2022
Xét ΔMNP vuông tại M có MK là đường cao
nên \(PM^2=PK\cdot PN\)
=>x(x+6)=16
=>x=2
15 tháng 8
a: ΔMDN vuông tại D
=>\(MD^2+DN^2=MN^2\)
=>\(MN^2=6^2+8^2=36+64=100=10^2\)
=>MN=10(cm)
Xét ΔDNM vuông tại D có \(\sin DMN=\frac{DN}{MN}=\frac{6}{10}=\frac35\)
nên \(\hat{DMN}\) ≃36 độ 52p
b: Xét ΔMDN vuông tại D có DA là đường cao
nên \(MA\cdot MN=MD^2\left(1\right)\)
Xét ΔMDP vuông tại D có DB là đường cao
nên \(MB\cdot MP=MD^2\left(2\right)\)
Từ (1),(2) suy ra \(MA\cdot MN=MB\cdot MP\)
c: Xét ΔMIN vuông tại I và ΔMKP vuông tại K có
\(\hat{IMN}\) chung
Do đó: ΔMIN~ΔMKP
=>\(\frac{MI}{MK}=\frac{MN}{MP}\)
=>\(\frac{MI}{MN}=\frac{MK}{MP}\)
Xét ΔMIK và ΔMNP có
\(\frac{MI}{MN}=\frac{MK}{MP}\)
góc IMK chung
Do đó: ΔMIK~ΔMNP
=>\(\hat{MIK}=\hat{MNP}\left(3\right)\)
ta có: \(MA\cdot MN=MB\cdot MP\)
=>\(\frac{MA}{MP}=\frac{MB}{MN}\)
Xét ΔMAB và ΔMPN có
\(\frac{MA}{MP}=\frac{MB}{MN}\)
góc AMB chung
Do đó: ΔMAB~ΔMPN
=>\(\hat{MBA}=\hat{MNP}\left(4\right)\)
Từ (3),(4) suy ra \(\hat{MBA}=\hat{MIK}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên BA//KI
SV
Sinh Viên NEU
CTVVIP
8 tháng 11 2023
Áp dụng định lý Py-ta-go cho tam giác MNP vuông tại M:
\(MN^2+MP^2=NP^2\)
Thay số: \(7^2+MP^2=25^2\)
\(\Rightarrow MP=24\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông MNP, đường cao MH ta có:
\(MK.NP=MN.MP\)
Thay số: \(MK.25=7.24\Rightarrow MK=6,72\left(cm\right)\)
Áp dụng định lý Py - ta - go cho tam giác MNK vuông tại K ta có:
\(MK^2+NK^2=MN^2\)
Thay số: \(6,72^2+NK^2=7^2\Rightarrow NK=1,96cm\)
12 tháng 8 2016
ta sử dụng hệ thức lượng trong tam giác vuông
\(\frac{1}{MN^2}+\frac{1}{MP^2}=\frac{1}{AH^2}\)
mà MN=3MP/4
they vào ta đc : \(\frac{1}{\left(\frac{3}{4}MP\right)^2}+\frac{1}{MP^2}=\frac{1}{12^2}\)
<=> \(\frac{16}{9MP^2}+\frac{1}{MP^2}=\frac{1}{12^2}\)
<==> \(\frac{25}{9MP^2}=\frac{1}{12^2}\)=>\(MP^2=\frac{12^2.15}{9}=240\)
=> MP=\(4\sqrt{15}\)
bài 10: gống cái trên :
tiếp : tính:\(NM=\frac{3}{4}MP=3\sqrt{15}\)
áp dungnj đl pita go ta có :
NP=\(\sqrt{MN^2+MP^2}=5\sqrt{15}\)
UT
18 tháng 4 2021
tự vẽ hình nhé
a, Xét \(\Delta\) MNP và \(\Delta\) HNM
< MNP chung
<NMP=<NHM(=90\(^0\) )
b,=> \(\dfrac{MN}{HN}=\dfrac{NP}{MN}\)
=> \(MN^2=NP\cdot NH\)
c, xét \(\Delta\) NMP vg tại M, áp dụng định lí Py - ta - go trong tam giác vg có
\(MN^2+MP^2=NP^2\)
=> \(NP^2=144\Rightarrow NP=12cm\)
Ta có \(MN^2=NH\cdot NP\)
Thay số:\(7,2^2=NH\cdot12\Rightarrow NH=4,32cm\)
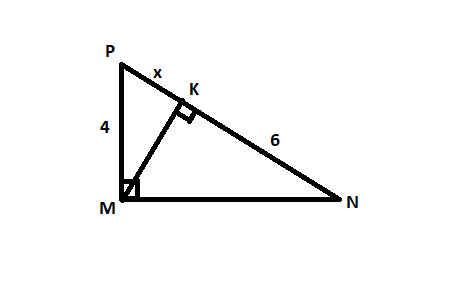
Áp dụng định lí Pytago vào ΔMPK vuông tại K, ta được:
\(MP^2=MK^2+KP^2\)
\(\Leftrightarrow MP^2=3^2+\left(2\sqrt{3}\right)^2=21\)
hay \(MP=\sqrt{21}\left(cm\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔMNP vuông tại M có MK là đường cao ứng với cạnh huyền NP, ta được:
\(MK^2=PK\cdot NK\)
\(\Leftrightarrow NK=\dfrac{12}{3}=4\left(cm\right)\)
Xét ΔMPK vuông tại K có
\(\cos\widehat{MPN}=\dfrac{PK}{MP}=\dfrac{3}{\sqrt{21}}=\dfrac{\sqrt{21}}{7}\)
Xét ΔMKN vuông tại K có
\(\tan\widehat{MNP}=\dfrac{MK}{KN}=\dfrac{2\sqrt{3}}{4}=\dfrac{\sqrt{3}}{2}\)