Helpp!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1 I wear colorful clothes during Tet Holiday
2 I will say happy new year to my mother
3 She won't ask for lucky money
4 I won't sweep the floor
5 He won't take the things related to the house out of water
1. I wear colorful clothes during Tet Holiday.
2. I will to say happy new year.....đoạn này mk hơi bí![]() .
.
3. She won't ask for lucky money.
4. I won't sweep the floor.
5. He won't take the things related to the house out of water.


Do M thuộc d nên tọa độ có dạng: \(M\left(2+2t;3+t\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(2+2t;2+t\right)\)
\(\Rightarrow AM=\sqrt{\left(2+2t\right)^2+\left(2+t\right)^2}=\sqrt{5t^2+12t+8}\)
Mà \(AM=5\Rightarrow\sqrt{5t^2+12t+8}=5\)
\(\Rightarrow5t^2+12t+8=25\)
\(\Rightarrow5t^2+12t-17=0\Rightarrow\left[{}\begin{matrix}t=1\\t=-\dfrac{17}{5}\end{matrix}\right.\)
Với \(t=1\Rightarrow M\left(4;4\right)\) loại do hoành độ dương
Với \(t=-\dfrac{17}{5}\Rightarrow M\left(-\dfrac{24}{5};-\dfrac{2}{5}\right)\) thỏa mãn
M thuộc D nên tọa độ M có dạng (2+2a;3+a) . Vì M có hoành độ âm nên a<-1.
Theo bài ra, ta có : \(AM=5\Leftrightarrow\sqrt{\left(2+2a\right)^2+\left(2+a\right)^2}=5\)
\(\Leftrightarrow5a^2+12a-17=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=1\left(loại\right)\\a=-\dfrac{17}{5}\left(nhận\right)\end{matrix}\right.\)
Với a = -17 /5
=> \(M\left(-\dfrac{24}{5};-\dfrac{2}{5}\right)\)


1 Tet is the most important festival in Viet Nam, therefore, most Vietnamese return home for Tet.
2 If you are Vietnamese, you should know the story of Chung cakes
3 All the students love the principal because he is very kind
4 Although Mr.Lam was very busy, he spent the whole day at the La Mat Village festival
5 ...... listening to pop music to watching TV after school

A.
\(C_2H_2+H_2\xrightarrow[t^o]{Pd}C_2H_4\\ C_2H_4+H_2\xrightarrow[t^o]{Ni}C_2H_6\)


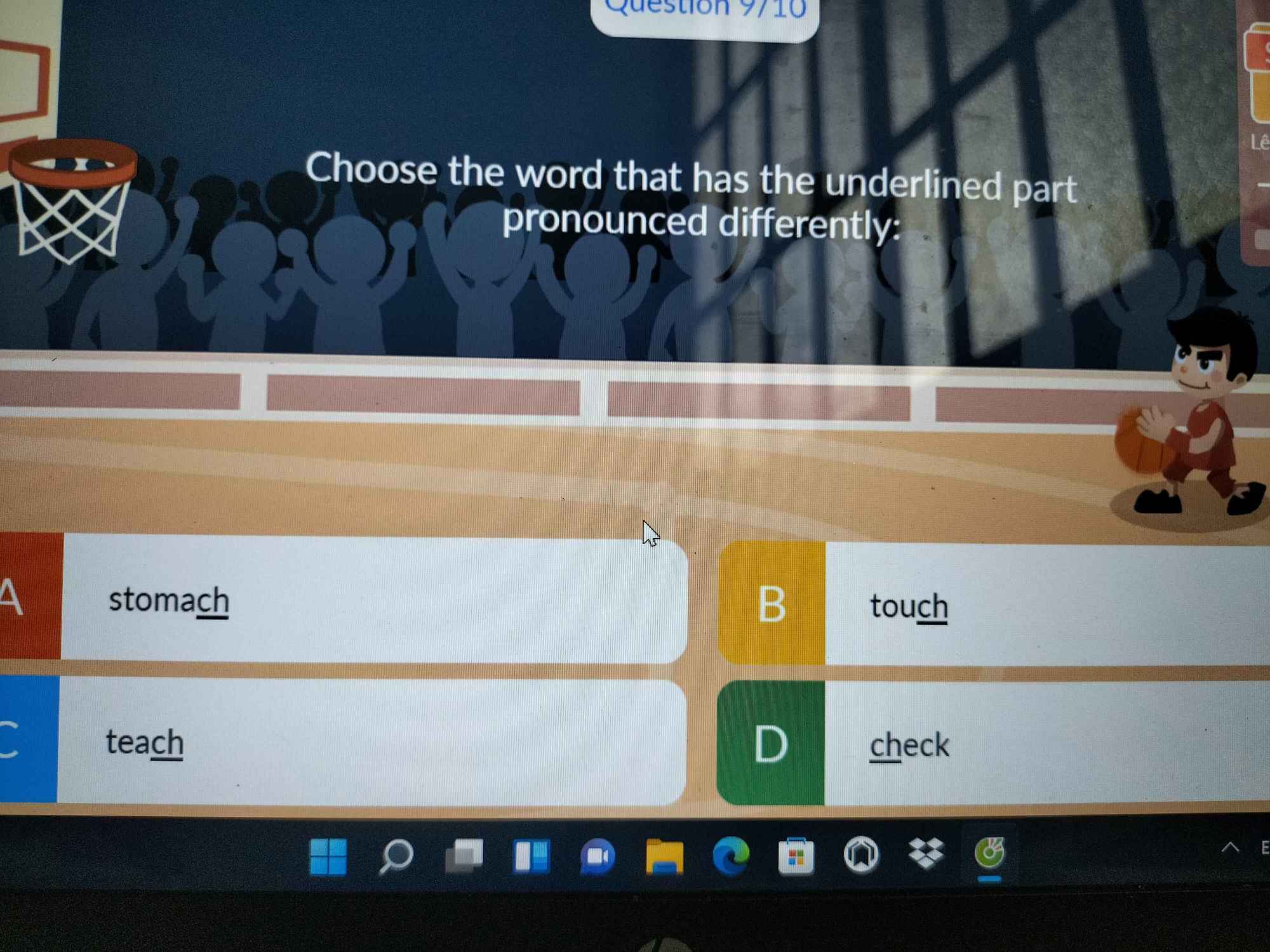
 Helpp
Helpp





Bạn cần giúp gì nhỉ? <3