Chứng minh:
a\(⋮̸\) m ; b \(⋮\)m thì ( a + b ) \(⋮̸\) m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NK
1
22 tháng 4 2021
a.m+2>n+2
Ta có: m >n
=>m+2 > n+2 (cộng hai vế với 2)
do đó m+2>n+2
b, -2m < -2n
Ta có: m > n
=> -2m < -2n (nhân hai vế với -2)
do đó -2m<-2n
c,2m-5>2n-5
Ta có: m>n
=>2m>2n (nhân hai vế với 2)
=>2m-5>2n-5 ( cộng hai vế với -5)
do đó 2m-5>2n-5
d,4-3m<4-3n
Ta có :m>n
=> -3m<-3n (nhân hai vế với -3)
=> 4-3m<4-3n (cộng 2 vế với 4)
13 tháng 11 2021
a, Vì \(\left\{{}\begin{matrix}\widehat{MAB}=\widehat{MAC}\\AB=AC\\AM.chung\end{matrix}\right.\) nên \(\Delta ABM=\Delta ACM\left(c.g.c\right)\)
b, Vì \(\Delta ABM=\Delta ACM\) nên \(\left\{{}\begin{matrix}\widehat{AMB}=\widehat{AMC}\\BM=MC\end{matrix}\right.\)
Mà \(\widehat{AMB}+\widehat{AMC}=180^0\Rightarrow\widehat{AMB}=\widehat{AMC}=90^0\)
Vậy \(AM\perp BC\) và M là trung điểm BC
25 tháng 2 2022
a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
Suy ra: AE=AF
hay ΔAEF cân tại A
9 tháng 1 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là tia phân giác của góc BAC
27 tháng 12 2021
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AC//BE
KV
5 tháng 12 2023
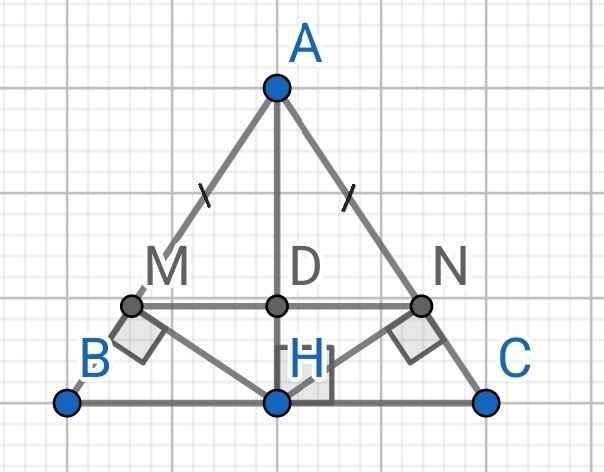
a) Xét hai tam giác vuông: ∆ABH và ∆ACH có:
AB = AC (gt)
AH là cạnh chung
⇒ ∆ABH = ∆ACH (cạnh huyền - cạnh góc vuông)
b) Do ∆ABH = ∆ACH (cmt)
⇒ ∠BAH = ∠CAH (hai góc tương ứng)
⇒ ∠MAH = ∠NAH
Xét hai tam giác vuông: ∆AMH và ∆ANH có:
AH là cạnh chung
∠MAH = ∠NAH (cmt)
⇒ ∆AMH = ∆ANH (cạnh huyền - góc nhọn)
c) Do ∆AMH = ∆ANH (cmt)
⇒ MH = NH (hai cạnh tương ứng)
Do ∆ABH = ∆ACH (cmt)
⇒ BH = CH (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆MBH và ∆NCH có:
BH = CH (cmt)
MH = NH (cmt)
⇒ ∆MBH = ∆NCH (cạnh huyền - cạnh góc vuông)
d) Do ∆AMH = ∆ANH (cmt)
⇒ ∠MHA = ∠NHA (hai góc tương ứng)
⇒ HA là tia phân giác của ∠MHN
e) Gọi D là giao điểm của MN và AH
Do ∆AMH = ∆ANH (cmt)
⇒ ∠MAH = ∠NAH (hai góc tương ứng)
⇒ ∠MAD = ∠NAD
Do ∆AMH = ∆ANH (cmt)
⇒ AM = AN (hai cạnh tương ứng)
Xét ∆AMD và ∆AND có:
AM = AN (cmt)
∠MAD = ∠NAD (cmt)
AD là cạnh chung
⇒ ∆AMD = ∆AND (c-g-c)
⇒ ∠AMD = ∠AND (hai góc tương ứng)
⇒ ∠AMN = ∠ANM
∆AMN có:
∠AMN + ∠ANM + ∠MAN = 180⁰ (tổng ba góc trong ∆AMN)
⇒ ∠AMN = ∠ANM = (180⁰ - ∠MAN) : 2
= (180⁰ - BAC) : 2 (1)
Do ∆ABH = ∆ACH (cmt)
⇒ ∠ABH = ∠ACH (hai góc tương ứng)
⇒ ∠ABC = ∠ACB
∆ABC có:
∠BAC + ∠ABC + ∠ACB = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (2)
Từ (1) và (2) ⇒ ∠AMN = ∠ABC
Mà ∠AMN và ∠ABC là hai góc đồng vị
⇒ MN // BC
5 tháng 10 2021
a,Vì \(\left\{{}\begin{matrix}AM=MD\\BQ=QC\end{matrix}\right.\) nên MQ là đtb hình thang ABCD \(\Rightarrow MQ//AB\left(1\right)\)
Vì \(\left\{{}\begin{matrix}AM=MD\\DN=NB\end{matrix}\right.;\left\{{}\begin{matrix}BQ=QC\\AP=PC\end{matrix}\right.\) nên MN,PQ lần lượt là đtb các tam giác ABD,ABC
\(\Rightarrow MN//AB\left(2\right);PQ//AB\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow MN;MQ;PQ\) trùng nhau hay M,N,P,Q thẳng hàng
b,Ta có \(NP=MQ-MN-PQ\)
\(\Rightarrow NP=\dfrac{AB+CD}{2}-\dfrac{AB}{2}-\dfrac{AB}{2}\left(t/c.đường.trung.bình\right)\\ \Rightarrow NP=\dfrac{CD-AB}{2}\)
20 tháng 4 2023
Sửa đề: ΔABC cân tại A
a: D nằm trên trung trực của AB,AC
=>DA=DB; DA=DC
=>DB=DC
b: ΔABC cân tại A
ma AM là trung tuyến
nên AM là trung trực của CB
mà D nằm trên trung trực của BC
nên A,M,D thẳng hàng
Ta có : a⋮̸ m ; b ⋮m
Cho: a=m.k+t (m là số chia,k là thương ,t là số dư)
b=m.h(m là số chia ,k là thương)
=>a+b=(m.k+t)+(m.h)
=m.k+t+m.h
=m.(k+h)+t
Vì : m.(k+h) ⋮ m và t<m(vì số dư luôn bé thua số chia)
=>m.(k+h)+t ⋮̸ m
=>(a+b)⋮̸ m
Ví dụ:
a = 9
b = 10
m = 5
a \(⋮̸\)m , b \(⋮\)m , => ( a + b ) \(⋮̸\)m