Xác định đồng biến, nghịch biến của hàm số y = x∧4 + 2x∧2 - 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - 1; + \infty } \right)\) nên hàm số đồng biến trong khoảng \(\left( { - 1; + \infty } \right)\). Trong khoảng \(\left( { - \infty ; - 1} \right)\) thì hàm số nghich biến.
Bảng biến thiên:
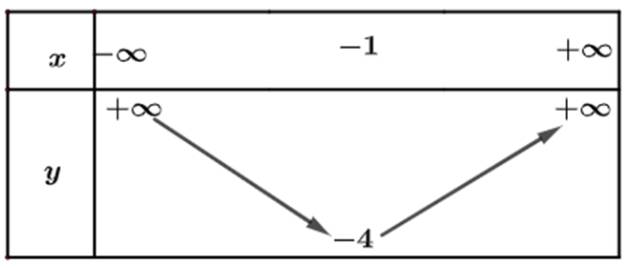
b) Từ đồ thị ta thấy đồ thị hàm số đi lên trong khoảng \(\left( { - \infty ;1} \right)\) nên hàm số đồng biến trong khoảng \(\left( { - \infty ;1} \right)\). Trong khoảng \(\left( {1; + \infty } \right)\) thì hàm số nghịch biến.
Bảng biến thiên:
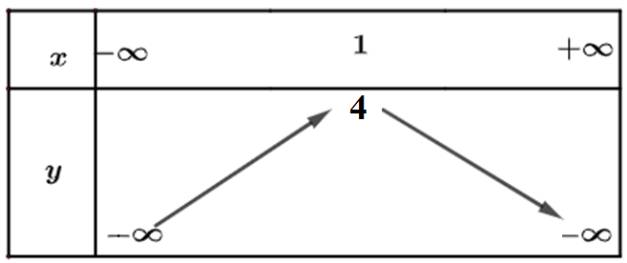

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

a) Để hàm số đồng biến thì k(k-3)>0
\(\Leftrightarrow\left[{}\begin{matrix}k>3\\k< 0\end{matrix}\right.\)
b) Để hàm số nghịch biến thì k(k-3)<0
hay 0<x<3

a: TXĐ: D=R\{-1}
\(y'=\dfrac{\left(x+m\right)'\left(x+1\right)-\left(x+1\right)'\left(x+m\right)}{\left(x+1\right)^2}\)
\(=\dfrac{x+1-x-m}{\left(x+1\right)^2}=\dfrac{1-m}{\left(x+1\right)^2}\)
Để hàm số nghịch biến trên từng khoảng xác định thì \(y'< 0\forall x\)
=>\(\dfrac{1-m}{\left(x+1\right)^2}< 0\)
=>1-m<0
=>m>1
b: TXĐ: D=R\{m}
\(y=\dfrac{2x-3m}{x-m}\)
=>\(y'=\dfrac{\left(2x-3m\right)'\left(x-m\right)-\left(2x-3m\right)\left(x-m\right)'}{\left(x-m\right)^2}\)
\(=\dfrac{2\left(x-m\right)-\left(2x-3m\right)}{\left(x-m\right)^2}=\dfrac{2x-2m-2x+3m}{\left(x-m\right)^2}\)
\(=\dfrac{m}{\left(x-m\right)^2}\)
Để hàm số đồng biến trên từng khoảng xác định thì \(y'>0\forall x\)
=>\(\dfrac{m}{\left(x-m\right)^2}>0\)
=>m>0




\(y'=4x^3+4x=0\Leftrightarrow4x\left(x^2+1\right)=0\Rightarrow x=0\)
\(y'>0\) khi \(x>0\)
\(y'< 0\) khi \(x< 0\)
Hàm nghịch biến trên \(\left(-\infty;0\right)\) ; đồng biến trên \(\left(0;+\infty\right)\)