MỌI NGƯỜI ƠI GIÚP MÌNH VỚI 😢😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KL
2
10 tháng 10 2021
d: ta có: \(C=3+3^3+3^5+...+3^{1991}\)
\(=3\left(1+3^2+3^4\right)+...+3^{1987}\left(1+3^2+3^4\right)\)
\(=91\cdot\left(3+...+3^{1987}\right)⋮13\)
DV
2
24 tháng 8 2021
Bài 2:
a: \(201^3=8120601\)
b: \(199^3=7880599\)
c: \(52^3-8=140600\)
d: \(23^3-27=12140\)
e: \(99^3=970299\)
f: \(62\cdot58=3596\)
24 tháng 8 2021
Bài 1:
a: \(\left(2x+y\right)^2-\left(y-2x\right)^2\)
\(=4x^2+4xy+y^2-y^2+4xy-4x^2\)
=8xy
b: \(\left(5x+5\right)^2+10\cdot\left(x-3\right)\left(x+1\right)+x^2-6x+9\)
\(=\left(5x+5\right)^2+2\cdot\left(5x+5\right)\cdot\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(6x+2\right)^2\)
\(=36x^2+24x+4\)
c: \(\left(x-y\right)^3+3xy\left(x-y\right)\)
\(=x^3-3x^2y+3xy^2-y^3+3x^2y-3xy^2\)
\(=x^3-y^3\)
d: \(\left(1-2x\right)\left(1+2x+4x^2\right)+8\left(x-1\right)\left(x^2+x+1\right)\)
\(=1-8x^3+8\left(x^3-1\right)\)
\(=1-8x^3+8x^3-8\)
=-7
19 tháng 8 2021
a: Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=4\)
\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9x^2+18x+9=4\)
\(\Leftrightarrow45x=-5\)
hay \(x=-\dfrac{1}{9}\)
b: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Leftrightarrow x^3-25x-x^3-8=17\)
\(\Leftrightarrow-25x=25\)
hay x=-1
TL
2
16 tháng 11 2021
Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.
11 tháng 7 2023
A=2(1+2)+2^3(1+2)+...+2^2009(1+2)
=3(2+2^3+...+2^2009) chia hết cho 3
A=2(1+2+2^2)+2^4(1+2+2^2)+...+2^2008(1+2+2^2)
=7(2+2^4+...+2^2008) chia hết cho 7
DV
2
19 tháng 8 2021
a) \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=\left(3x^2-6x+3\right)-\left(x^2+2x+1\right)+2\left(x^2-9\right)-\left(4x^2+12x+9\right)-5+20x\)
\(=-30\)
b) \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x\left(x^2+4x+4\right)+\left(4x^2+4x+1\right)+\left(x^3-3x^2+9x+3x^2-9x+27\right)-1\)
\(=27\)
19 tháng 8 2021
a: Ta có: \(A=3\left(x-1\right)^2-\left(x+1\right)^2+2\left(x-3\right)\left(x+3\right)-\left(2x+3\right)^2-\left(5-20x\right)\)
\(=3x^2-6x+3-x^2-2x-1+2x^2-18-4x^2-12x-9-5+20x\)
\(=-30\)
b: Ta có: \(B=-x\left(x+2\right)^2+\left(2x+1\right)^2+\left(x+3\right)\left(x^2-3x+9\right)-1\)
\(=-x^3-4x^2-4x+4x^2+4x+1+x^3+27-1\)
=27
DV
3
31 tháng 8 2021
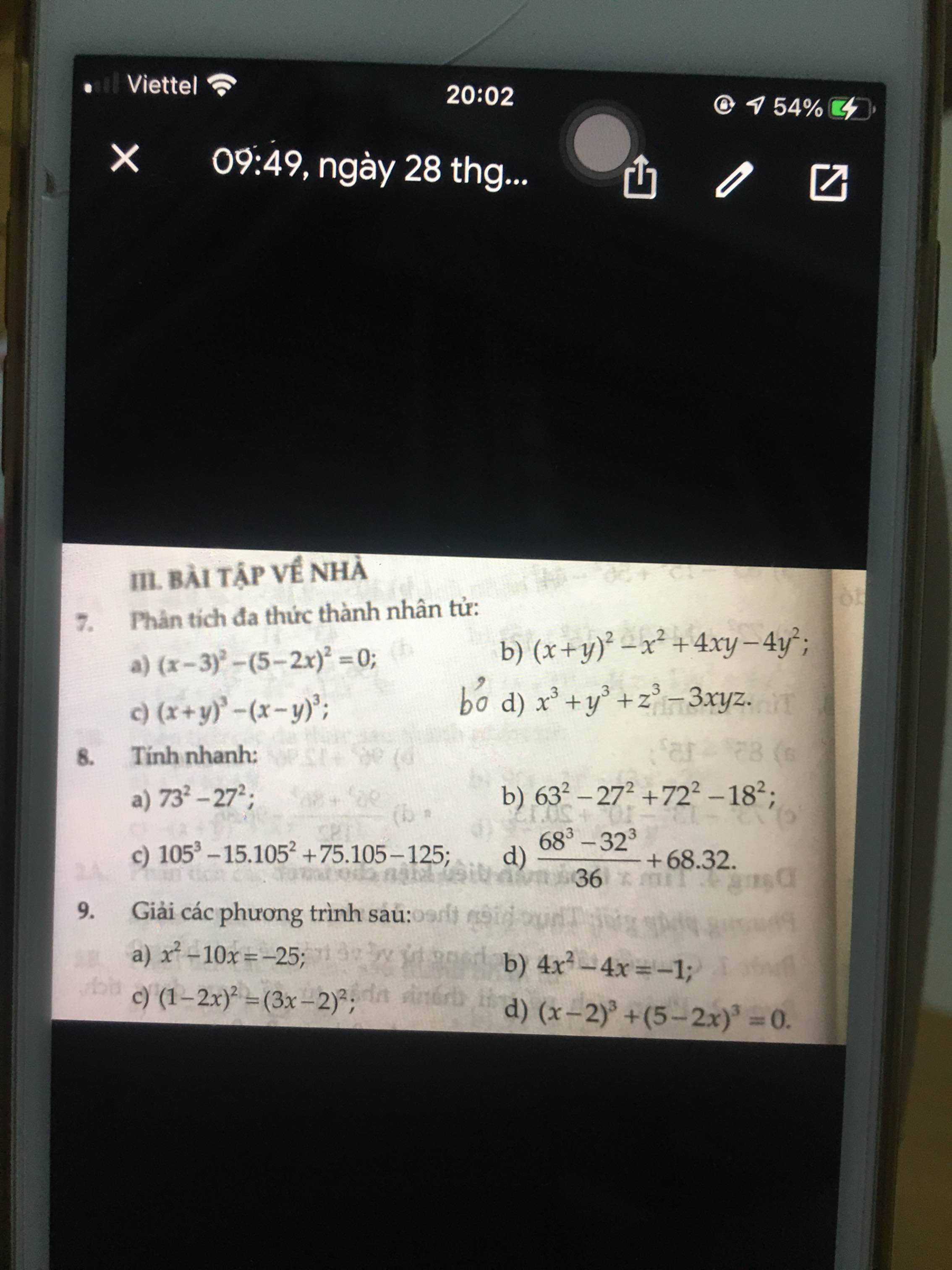
Bài 9:
a: Ta có: \(x^2-10x=-25\)
\(\Leftrightarrow x^2-10x+25=0\)
\(\Leftrightarrow x-5=0\)
hay x=5
b: ta có: \(4x^2-4x=-1\)
\(\Leftrightarrow4x^2-4x+1=0\)
\(\Leftrightarrow2x-1=0\)
hay \(x=\dfrac{1}{2}\)
c: Ta có: \(\left(2x-1\right)^2=\left(3x-2\right)^2\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(2x-1\right)^2=0\)
\(\Leftrightarrow\left(3x-2-2x+1\right)\left(3x-2+2x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(5x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)
DV
2
31 tháng 8 2021
Bài 8:
a: \(73^2-27^2=\left(73-27\right)\left(73+27\right)=4600\)
b: \(63^2-27^2+72^2-18^2\)
\(=\left(63-18\right)\left(63+18\right)+\left(72-27\right)\left(72+27\right)\)
\(=45\cdot\left(63+18+72+27\right)\)
\(=45\cdot180=8100\)
DV
1
2 tháng 9 2021
b: Ta có: \(\left(x+y\right)^2-x^2+4xy-4y^2\)
\(=\left(x+y\right)^2-\left(x-2y\right)^2\)
\(=\left(x+y-x+2y\right)\left(x+y+x-2y\right)\)
\(=3y\cdot\left(2x-y\right)\)
c: Ta có: \(\left(x+y\right)^3-\left(x-y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3\)
\(=2y^3+6x^2y\)
\(=2y\left(3x^2+y^2\right)\)
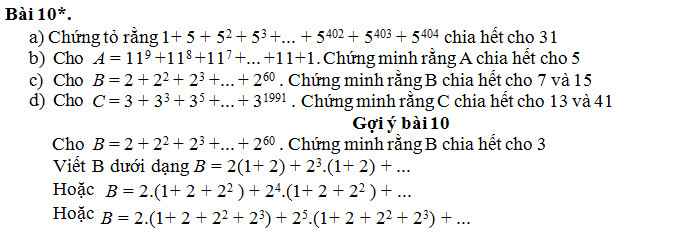
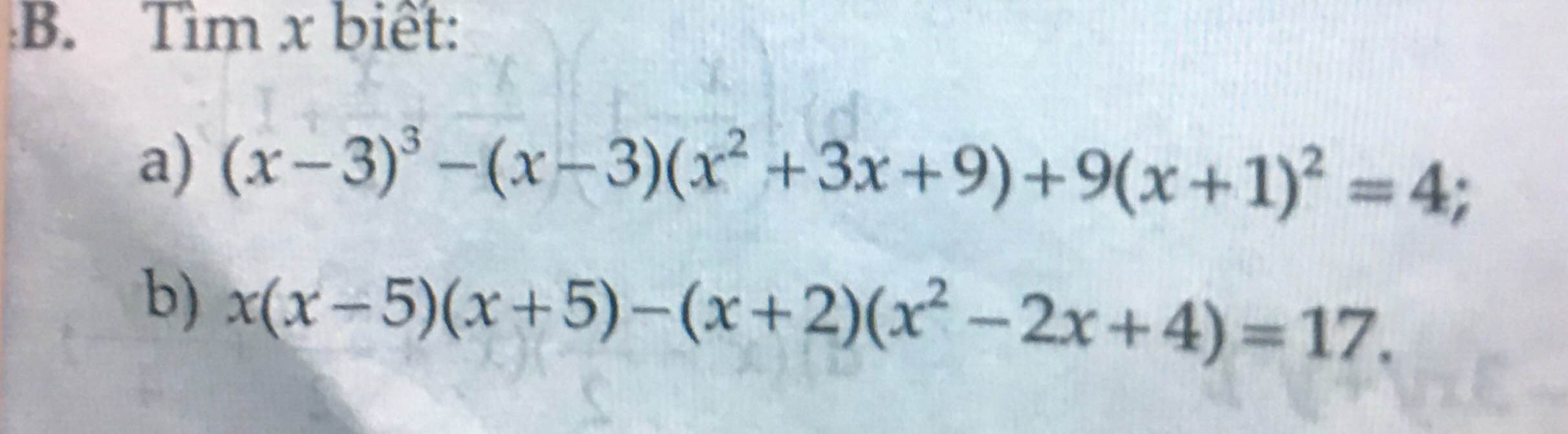
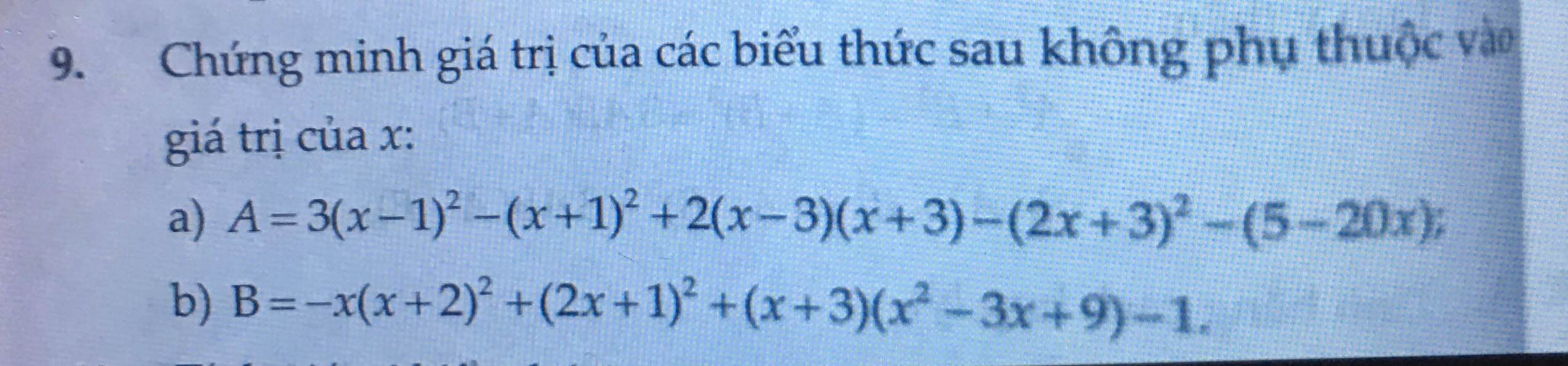
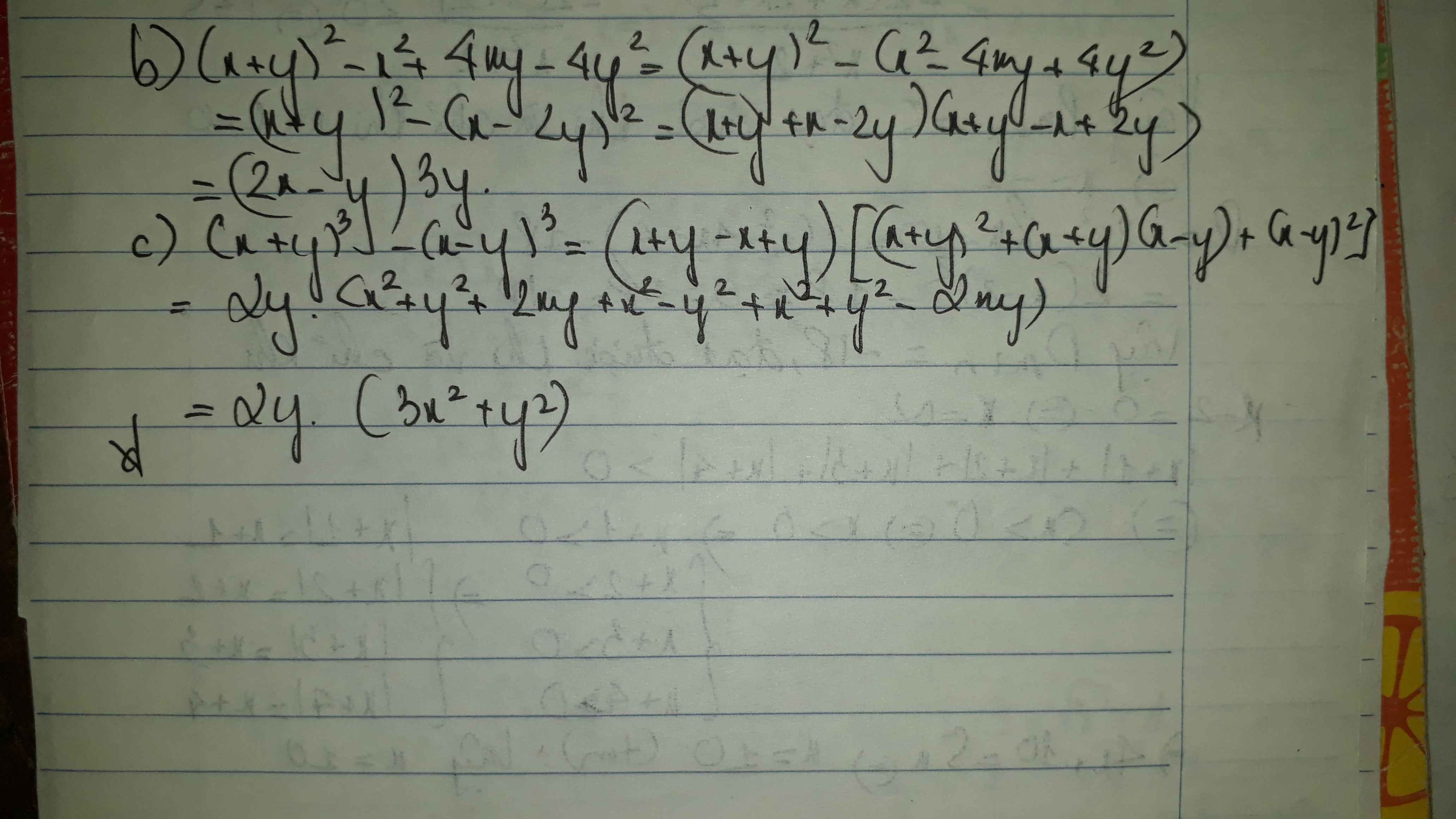
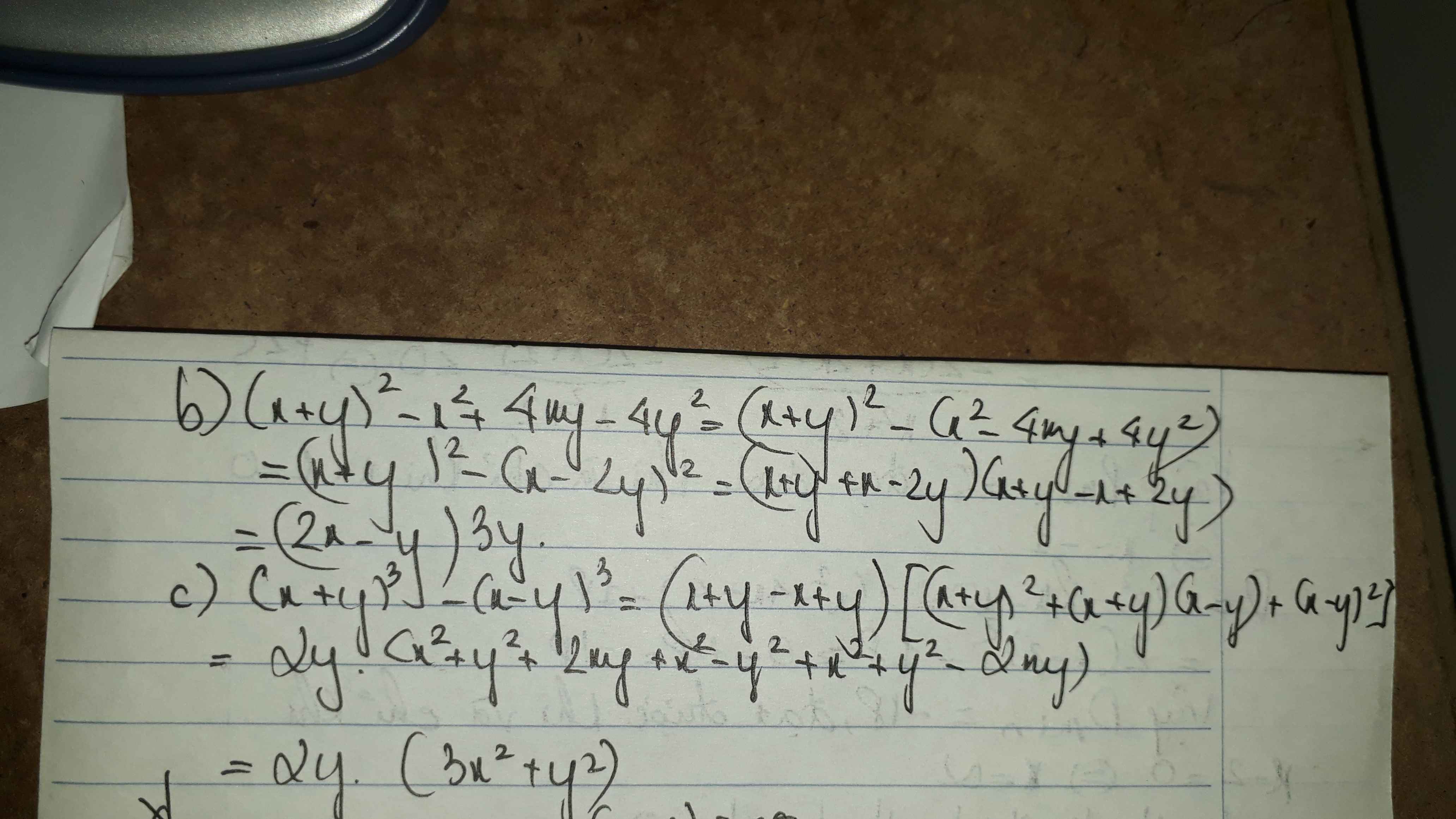
4)
a/ A(x)= -45-x3+4x2+ 5x+9+4x5-6x2-2
A(x)= -x3-2x2+5x+7
b/ B(x)= -3x4-2x3 +10x2 -8x+5x3-7-2x3+8x
B(x)= -3x4 +x3+10x2 -7
A(x)= -x3-2x2+5x+7
B(x)= -3x4 +x3+10x2 -7
b) P(x) = A(x)+B(x)= -x3-2x2+5x+7-3x4 +x3+10x2 -7= -3x4 +8x2+5x
Q(x)= -x3-2x2+5x+7- (-3x4 +x3+10x2 -7)= -x3-2x2+5x+7 + 3x4-x3 - 10x2 + 7= -2x3-12x2+5x+ 14