Tính tổng Sn =2 +4 +6 + ....+2n .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 6 2019
Chọn D
S n = 2 2 + 1 2 2 + 2 + 2 4 + 1 2 4 + 2 + ... + 2 2 n + 1 2 2 n + 2 = 2 2 + 2 4 + ... + 2 2 n + 1 2 2 + 1 2 4 + ... + 1 2 2 n + 2 n = 4. 1 − 4 n 1 − 4 + 1 4 1 − 1 4 n 1 − 1 4 + 2 n = 4 n − 1 3 4 − 1 4 n + 2 n .
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
1. Áp dụng công thức tổng cấp số nhân:
\(S_n=u_1.\dfrac{q^n-1}{q-1}=2.\dfrac{2^n-1}{2-1}=2.\left(2^n-1\right)=2^{n+1}-2\)
2. \(\left\{{}\begin{matrix}u_2+u_5=12\\u_4+u_8=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(u_1+d\right)+\left(u_1+4d\right)=12\\\left(u_1+3d\right)+\left(u_1+7d\right)=22\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2u_1+5d=12\\2u_1+10d=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=2\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=1+\left(n-1\right)2=2n-1\)
\(\Rightarrow S_n=\dfrac{n\left(u_1+u_n\right)}{2}=\dfrac{n\left(1+2n-1\right)}{2}=n^2\)
3. \(\left\{{}\begin{matrix}u_1+u_2=4\\u_4+u_1=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1q=4\\u_1q^3+u_1=28\end{matrix}\right.\)
\(\Rightarrow\dfrac{q^3+1}{q+1}=\dfrac{28}{4}\Rightarrow q^2-q+1=7\)
\(\Rightarrow q^2-q-6=0\Rightarrow\left[{}\begin{matrix}q=3\\q=-2\end{matrix}\right.\)
DD
0
VN
2
9 tháng 9 2018
2 + 4 + 6 + 8 + ... + (2n - 2) + 2n
Giải : Khoảng cách giữa hai số hạng liên tiếp là 2 đơn vị
Số số hạng là : (2n - 2) : 2 + 1 = n ( số hạng )
Tổng số hạng là : (2n + 2) . n : 2 = n2 + n
9 tháng 9 2018
Số số hạng là
(2n-2):2 +1=n
tống số đầu và số cuối là
2n+2=2n+2
tổng sẽ là
n * (2n+2):2= n(n+1)
vậy tổng sẽ là n(n+1)
chúc bạn học tốt nhé
6 tháng 2 2017
f(x) = ax2 + bx + c
f(x - 1) = a(x - 1)2 + b(x - 1) + c = a(x2 - 2x + 1) + bx - b + c = ax2 - 2ax + a + bx - b + c
f(x) - f(x - 1) = (ax2 + bx + c) - (ax2 - 2ax + a + bx - b + c) = ax2 + bx + c - ax2 + 2ax - a - bx + b - c = 2ax - a + b
mà f(x) - f(x - 1) = 2x - 1
=> 2ax - a + b = 2x - 1
<=> 2ax - a + b - 2x + 1 = 0
<=> 2x(a - 1) - (a - 1) + b = 0
<=> (a - 1)(2x - 1) + b = 0
<=> a - 1 = 0 và b = 0
<=> a = 1 và b = 0
Chọn c tuỳ ý.
Chọn c = 0 => f(x) = x2
Đặt f(n) = n2
1 = f(1) - f(0)
3 = f(2) - f(1)
5 = f(3) - f(2)
. . .
2n - 1 = f(n) - f(n - 1)
S = 1 + 3 + 5 + . . . (2n - 1) = f(1) - f(0) + f(2) - f(1) + f(3) - f(2) + . . . + f(n) - f(n -1) = f(n) - f(0) = n2
Vậy S = 1 + 3 + 5 + . . . (2n - 1) = n2
DV
5
10 tháng 12 2017
x chia hết cho 20 ; x chia hết 35 và x< 500
24chia hết cho x; 36 chia hết x; 60 chia hết cho x và 1<x<10
10 tháng 12 2017
2)dãy trên có tất cả:(2n-2):2+1=n(số hạng)
(vì (2n-2):2+1=2(n-1):2+1=n-1+1=n)
2+4+6+...+2n=(2n+2)xn:2=n x( n+1)
câu 1 làm tương tự
DT
7 tháng 2 2022
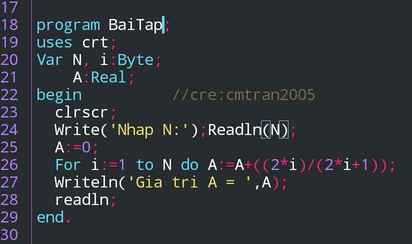
Thuật toán: B1: Nhập N;
B2: A <--- 0; i <--- 1;
B3: A <--- A + ((2*i)/(2*i+1));
B4: i <--- i + 1;
B5: Nếu i > N thì thông báo A rồi kết thúc.
B6: Quay lại bước 3;
DV
1
SSH: \(\frac{2n-2}{2}+1=\frac{2n}{2}-\frac{2}{2}+1=n-2+1=n-1\)
Tổng : \(\frac{\left(2n+2\right)\left(n-1\right)}{2}=\frac{2\left(n+1\right)\left(n-1\right)}{2}=\frac{2\left(n^2-1\right)}{2}=n^2-1\)
Tổng n số hạng đầu cấp số cộng có công sai: d = 2 và u1 = 2
\(\Rightarrow S=\frac{\left(2+2n\right).n}{2}\Leftrightarrow S=\left(1+n\right).n\)