Trong không gian với hệ trục cho điểm là trung điểm của đoạn , biết . Tọa độ điểm là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải:
Khoảng cách từ tâm đến trục Oz chính bằng bán kính R
Phương trình mặt cầu tâm và bán kính
![]()
Lời giải:
Phương trình trục Oz
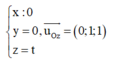
Ta có
![]()
Khoảng cách từ tâm I -> Oz là
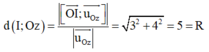
Vì (S) tiếp xúc với trục Oz Þ Phương trình cần tìm là ( S ) : x - 3 2 + y - 4 2 + z + 2 2 = 25

Đáp án A.
![]()
Mặt phẳng (P) qua I và vuông góc với Oy là:
![]()
=> bán kính mặt cầu tâm I và tiếp xúc với trục Oy là:
![]()
= 10
=> Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:
![]()

Đáp án D.
Mặt phẳng (Oxz): y = 0 nên d (I,(Oxz)) = 3
Vậy phương trình của mặt cầu là
![]()

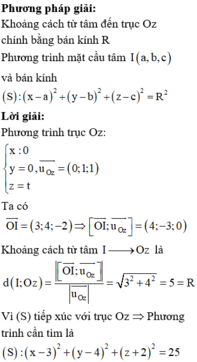


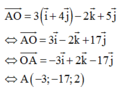

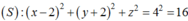
Tọa độ điểm \(N\):
\(\hept{\begin{cases}x_N=-8.2-2=-18\\y_N=0.2-\left(-6\right)=6\\z_N=8.2-11=5\end{cases}}\)
\(N\left(-18,6,5\right)\)
Chọn A.