Biết đường thẳng 7x + by = 0 là đường phân giác của góc phần tư thứ ba thì giá trị của b là ....
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đường phân giác của góc phần tư thứ hai là đồ thị của hàm số y = -x.
Khi đó: -8y = ax => -8. (-x) = ax => a = 8

Đáp án A
Gọi ![]() là điểm cố định cần tìm.
là điểm cố định cần tìm.
Ta có ![]()
![]() .
.
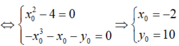
![]()
Lại có
![]()
Phương trình tiếp tuyến của ![]() có dạng
có dạng
![]() hay
hay
![]() .
.
Đường phân giác góc phần tư thứ nhất có phương trình d: y = x.
Vì
∆
vuông góc với d nên ta có ![]() .
.

a, Đường phân giác góc phần tư thứ nhất là một nửa đường thẳng x - y = 0 nằm ở góc phần tư thứ nhất
=> d nhận (1 ; -1) làm vecto pháp tuyến
=> PT đi qua M (-2 ; -5) là
x + 2 - y - 5 = 0 ⇔ x - y - 3 = 0
b, c, Lười lắm ko làm đâu :)

Hình vẽ:
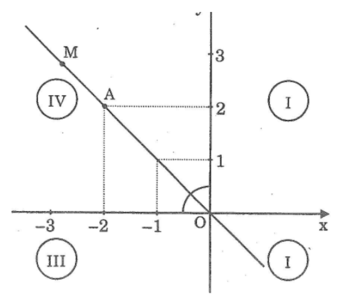
Điểm A có hoành độ bằng 2 thì điểm A có tung độ bằng - 2.

Hình vẽ:
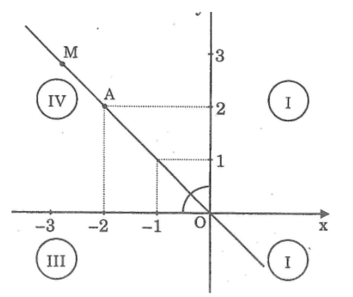
Điểm M nằm trên đường phân giác của các góc phần tư thứ II, IV thì có tung độ và hoành độ đối nhau

1) ax +8y =0 => y = -a/8 .x là phân giác góc phần tư thứ 2 khi -a /8 = -1 => a =8 ; ( y = -x)
2) OM = OA -AM = 5 -2 =3
pi ta - go cho MOC vuông tại M => MC2 = OC2 - OM2 = 52 - 32 = 16
=> MC =4 => CD = 8
SACBD = AB.CD/2 =10.8/2 =40 cm2
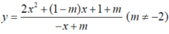 có đồ thị
và A là điểm cố định có hoành độ âm của
. Giá trị của để tiếp tuyến tại A của
vuông góc với đường phân giác góc phần tư thứ nhất là
có đồ thị
và A là điểm cố định có hoành độ âm của
. Giá trị của để tiếp tuyến tại A của
vuông góc với đường phân giác góc phần tư thứ nhất là
7x + by = 0 => y = \(-\frac{7}{b}\)x ( b khác 0)
đường phân giác của góc phần tư thứ ba là ý = x
=> -7/b = 1 => b = -7