mn cho mk hỏi đường xiên và hình chiếu là j z
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


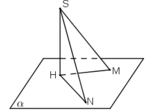
Giả sử ta có hai đường xiên SM, SN và các hình chiếu HM, HN của chúng trên mp (α).
Vì SH ⊥ mp(α)
⇒ SH ⊥ HM và SH ⊥ HN
⇒ ΔSHN và ΔSHM vuông tại H.
Áp dụng định lí Py-ta- go vào hai tam giác vuông này ta có:
⇒ S M 2 = S H 2 + H M 2 ; v à S N 2 = S H 2 + H N 2 . a ) S M = S N ⇔ S M 2 = S N 2 ⇔ H M 2 = H N 2 ⇔ H M = H N . b ) S M > S N ⇔ S M 2 > S N 2 ⇔ H M 2 > H N 2 ⇔ H M > H N .

a) Giả sử ta có hai đường xiên SA, SB và các hình chiếu HA, HB của chúng trên mp(α)
Giả sử HA = HB
Vì SH ⊥ mp(α) nên SH ⊥ HA và SH ⊥ SB và các tam giác SHA, SHB là các tam giác vuông. Hai tam giác vuông SHA, SHB có canh SH chung và HA = HB nên :
ΔSHA = ΔSHB SA = SB
Ngược lại nếu SA = SB thì ΔSHA = ΔSHB ⇒ HA = HB
Kết quả, ta có HA = HB SA= SB (đpcm)
b) Giả sử có hai đường xiên SA, SC và các hình chiếu HA, HC của chúng trên mp(α) với giả thiết HC > HA.
Trên đoạn HC, lấy điểm B' sao cho HA' = HA ⇒ HC > HA'. Như vậy, theo kết quả câu a) ta có SA' = SA. Ta có trong các tam giác vuông SHB', SHC thì :
SC2= SH2 + HC2
SA2 = SH2 + HA2
Vì HC > HA' nên SC2 > SA2 ⇒ SC > SA
Suy ra SC > SA
Như vậy HC > HA ⇒ SC > SA
Lí luận tương tự, ta có : SC > SA ⇒ HC > HA
Kết quả : HC > HA ⇔ SC > SA
a) Gọi SN là một đường xiên khác. Xét hai tam giác vuông SHM và SHN có SH chung. Nếu SM = SN => tam giác SHM = tam giác SHN => HM = HN, ngược lại nếu HM = HN thì tam giác SHM = tam giác SHNSM => SM = SN.
b) Xét tam giác vuông SHM và SHN có SH chung. Nếu SN > SM thì \(HN^2-SN^2-SH^2\) => \(SM^2-SH^2=HM^2\) => HN > HM. Chứng minh tương tự cho chiều ngược lại.

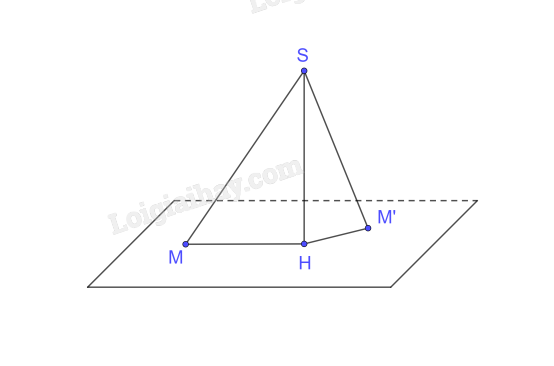
a)
+) Giả sử SM = SM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M'^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà SM = SM’ nên MH = MH’
+) Giả sử HM = HM’
Xét tam giác SHM vuông tại H có
\(S{M^2} = S{H^2} + M{H^2}\) (định lí Pytago)
Xét tam giác SHM’ vuông tại H có
\(S{M'^2} = S{H^2} + M'{H^2}\) (định lí Pytago)
Mà HM = HM’ nên SM = SM’
b) \(\begin{array}{l}MH > M'H \Leftrightarrow M{H^2} > M'{H^2}\\ \Leftrightarrow M{H^2} + S{H^2} > M'{H^2} + S{H^2} \Leftrightarrow S{M^2} > S{{M'}^2} \Leftrightarrow SM > SM'\end{array}\)

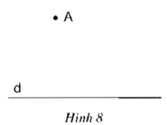
Sau khi vẽ theo yêu cầu đề bài, ta có:
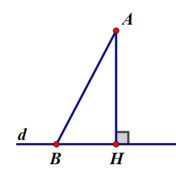
- Kẻ AH ⊥ d, H ∈ d ⇒ H là hình chiếu của A trên d
- Trên d lấy điểm B ≠ H . Nối AB ⇒ AB là đường xiên từ A đến d
Hình chiếu của đường xiên AB trên d là HB

tròn 1 điểm:33333 chế lại làm theo định lý pytago
ta có BH^2=AB^2-AH^2( áp dụng định lý pytago)
HC^2=AC^2-AH^2( áp dụng định lý pytago)
vì AB>AC=> AB^2>AC^2=> AB^2-AH^2>AC^2-AH^2=> BH^2>HC^2 => BH>CH (BH,CH>0)
làm thêm thui chứ cách của bạn ngắn hơn và đúng:33333

bài này ko cần pytago cx đc:
Ta có:
CB=CD
=> FB<CD ( F nằm trên đường thẳng CB)(1)
theo đề suy ra được : tam giác EFD nằm trong tam giác EBD
<=>FD<CB ( vì FD là cạnh nằm trong tam giác và tiếp với đường cao tam giác ngoài)(2)
Từ (1) và (2) suy ra : CD+CB>FD+FB( đpcm)
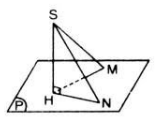

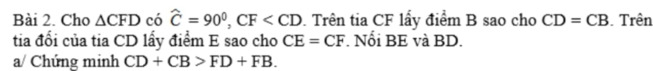
Xét tam giác ABC cân tại A Gọi D là điểm bất kì của cạnh đáy BC Kẻ đường cao AH ta có :
- Nếu \(D\equiv B\) hoặc C thì AD = AB = AC
- Nếu \(D\equiv H\) thì AD < AB ( hoặc AD < AC )
- Nếu D không trùng B ; C ; H giả sử D nằm giữa D và H thì trong tam giác ABH có BH và DH lần lượt là hình chiếu của AB và AD
Ta có : HD < HB nên suy ra AD < AB
Từ 3 điều trên trong 1 tam giác cân độ dài đoạn thẳng nối đỉnh đối diện với đáy và một điểm bất kỳ của cạnh đáy nhỏ hơn hoặc bằng độ dài của cạnh bên ( đpcm )
+ Đoạn AH gọi là đoạn vuông góc hay đường vuông góc
+ Đoạn AB gọi là đường xiên
+ Đoạn HB gọi là hình chiếu của đường xiên AB lên đường thẳng ra